- wichtiger Brüche wie 1/2, 1/4, 1/8 oder 1/3 und 2/3,
- der Gleichwertigkeit von Brüchen wie 1/2 = 2/4,
- der Addition und Subtraktion von Brüchen wie 1/2 + 1/4 = 3/4.
|
|
Brüche werden üblicherweise anhand des bekannten Kuchenmodells eingeführt. Die Vorteile dieses Modells liegen in der Veranschaulichung
|
|
Dahingegen hat das Streifenmodell den Vorteil, dass
|
Übungsaufgabe:
Annika und Peter bekommen an Weihnachten von ihrer Oma Geld geschenkt. Da Annika schon 14 Jahre alt ist und Peter erst 5, bekommt sie deutlich mehr, nämlich dreimal so viel wie Peter. Für beide zusammen hat die Oma 100 von der Bank geholt. Wie viel erhält nun jeder?1. Lösungsweg: In Anlehnung an das herkömmliche Verteilen (eins für Annika, eins für Peter eins für Annika, eins für Peter ) erhält in diesem Fall Annika bei jeder Verteilrunde dreimal so viel wie Peter: eins für Peter, drei für Annika eins für Peter, drei für Annika . Damit die Handlung nicht zu viel Zeit in Anspruch nimmt, beginnen wir mit dem Verteilen von 10-Euro-Scheinen:
 |
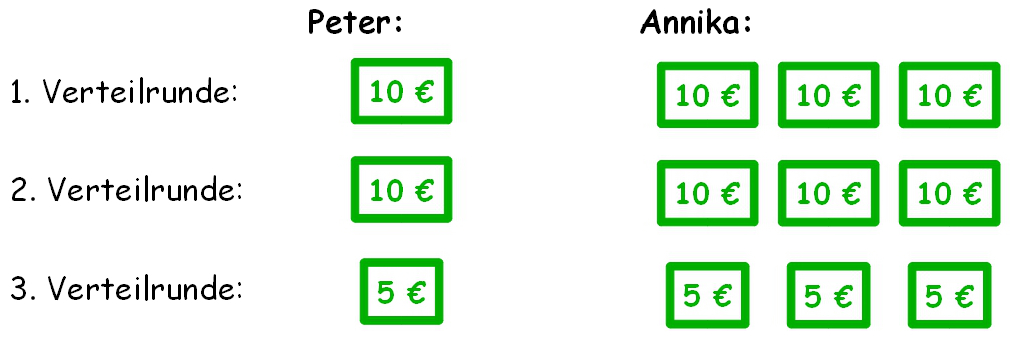Übungsaufgabe: Wie läuft der Verteilprozess ab, wenn Annika nur doppelt so viel bekommt wie Peter aber insgesamt wieder 100 zur Verfügung stehen? →Lösung
2. Lösungsweg: Wir kehren zurück zur ersten Aufgabe (Annika erhält dreimal so viel wie Peter). In Anbetracht der gefundenen Lösung bietet sich ein weiterer Lösungsweg an: Man hätte auch 4 gleichgroße Portionen aus den 100 herstellen können, um dann eine dieser Portionen Peter und die drei anderen Annika zu geben:
 |
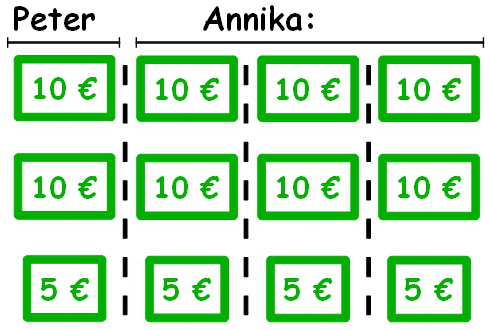Dieser Lösungsweg legt eine besondere Sprechweise nahe. Wir sagen:
Annika erhält 3 der 4 Teile von 100 .
Die Einführung dieser Sprechweise gestattet es uns, viele weitere Aufgaben zu formulieren und zu berechnen:
Darüber hinaus können wir auch nach den einzelnen Komponenten dieses Ausdrucks n der k Teile von s fragen:
|
(⇒ Das Gleiche als pdf-Datei) |
Übungsaufgabe: Lösen Sie in ähnlicher Weise die beiden anderen Aufgaben.
Mit der Zeit wird es einem lästig, den Ausdruck k der n Teile von x ist z auszuschreiben. Schüler wünschen sich bald eine kürzere Schreibweise auch wenn sie den Ausdruck immer noch ausführlich sprechen. Wir führen deshalb folgende Schreibweise ein:
|
Damit lassen sich die obigen Aufgaben wie folgt notieren:
= 60 / 5 von 1 Std. = 24 Min. von 1 Liter = 375 ml
 |
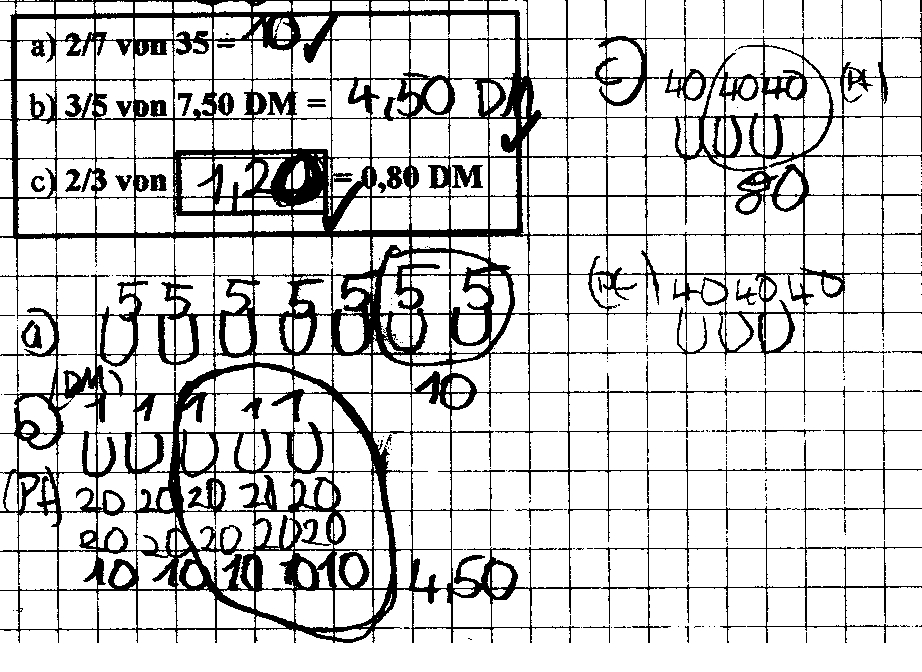Übungsaufgaben:
Die folgende Variation der Grundaufgabe a / b von c = dient dazu, das Verständnis von Brüchen weiter zu vertiefen:
Finde möglichst viele Lösungen für die Aufgabe:Schnell finden Kinder die Lösung 1 / 2 und vielleicht auch 30 / 60. Aber es gibt noch mehr:
Die Menge aller zu einem bestimmten Bruch (z.B. 1/2) synonymer Brüche bezeichnet man als Bruchzahl (1/2 und 2/4 gehören also zur selben Bruchzahl).
Mathematisch gesehen sind Brüche zunächst nur geordnete Paare von natürlichen Zahlen n und m (mit m ≠ 0), für die es verschiedene Schreibweisen gibt: n/m oder 
oder auch (n,m). Durch die Synonymität der Brüche erhält diese Menge von Zahlenpaaren eine charakteristische Struktur. Mathematisch wird die Synonymität zweier Brüche und 
folgendermaßen definiert:
Die Grundrechenarten werden wie üblich definiert, und es lässt sich dann beweisen, dass jede Rechnung mit Brüchen stets auch mit dazu synonymen Brüchen durchgeführt werden kann, weil die Ergebnisse dieser Rechnungen dann ebenfalls zueinander synonym sind. Mathematisch formuliert heiß das:
Sind x, x', y, y' Brüche, so dass x = x' und y = y' ist, dann gilt auch x + y = x' + y' (-, ×, ÷ ebenso).
Auf die Frage Was ist 1/3 und 1/5 ? stellt sich im Operatormodell sofort die Gegenfrage Wovon 1/3 und 1/5 ?. Wir wählen also zunächst eine Bezugsgröße, von der die Schüler sowohl 1/3 als auch 2/5 berechnen können (wie etwa von 30, 90 oder von 60 Min.) und addieren anschließend die berechneten Werte:
Allgemein:
(mit nat. Zahlen n,m,r,s,u,w und m,s,w ≠ 0)
Wie ein Schüler im 4. Schuljahr die Aufgabe 3/4 + 1/5 gerechnet hat, zeigt folgender Ausschnitt aus einem Rechentest. Bemerkenswert ist der Fehler bei der ikonischen Darstellung von 1/5; offensichtlich benötigt der Schüler solche Darstellungen nicht mehr in voller Gänze.
 |
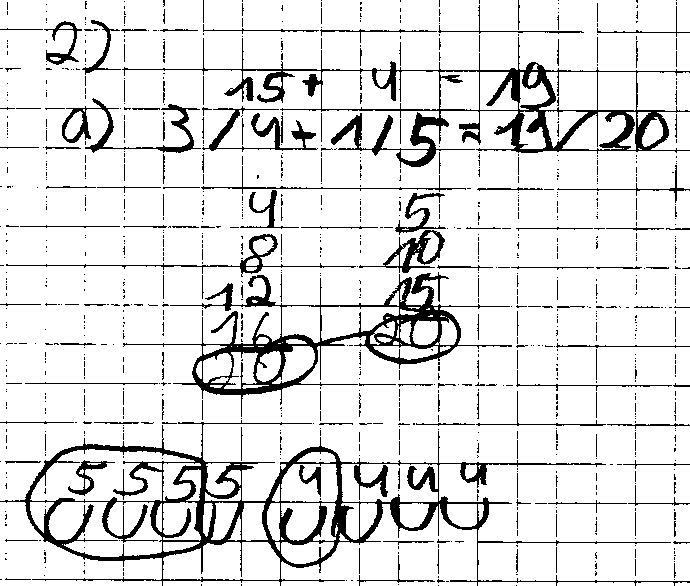Übungsaufgabe:
Die Multiplikation natürlicher Zahlen wird als wiederholte Addition definiert und in der Schule entsprechend eingeführt: 2×3=3+3. Dieser Gedanke ist auch auf die Multiplikation einer natürlichen Zahl mit einem Bruch anwendbar: 2×1/3=1/3+1/3. Aber wie sollte man das Produkt zweier Brüche verstehen, 1/2×1/3? Eine Möglichkeit haben wir schon oben beim Streifenmodell erwähnt. Hier wollen wir eine weitere Möglichkeit aufzeigen. Wir gehen jedoch nicht von der Frage aus, was das Produkt zweier Brüche ist, sondern untersuchen im Operatormodell Ausdrücke der Form
Zwar führen wir die Multiplikation damit (quasi) ein, aber eben nicht im ursprünglichen Sinne, sondern als nahe liegende Erweiterung des Operatormodells.
n/m von r/s von w
n der m Teile von r der s Teile von w
Didaktisch gehen wir ähnlich vor wie bei der Addition:
von von w = u
⇔
von
=  (mit nat. Zahlen n,m,r,s,u,w und m,s,w ≠ 0) |
Übungsaufgaben:
und nicht wie folgt definieren kann: von w)
· ( von w)
= u
⇔
·
=
= 3 · 1;
4 + 1
= 4 · 1;
5 + 1
= 5 · 1| a) | 2
+ 5
= 2
+ 5
|
b) | 2
· 5
= 2
· 5
|
Es gibt zwei Handlungsweisen des Dividierens: Aufteilen und Verteilen.
Gemeinsam ist beiden, dass eine Menge von bekanntem Umfang in gleich große Portionen zerlegt wird. Der Unterschied besteht darin, dass beim Aufteilen die Größe der Portionen bekannt ist und ihre Anzahl bestimmt wird, während man beim Verteilen die Anzahl kennt und die Größe der einzelnen Portionen bestimmt.
Das Aufteilen lässt sich rechnerisch durch wiederholte Subtraktionen darstellen, da bei der konkreten Handlung i.Allg. mehrfach Portionen vorgegebener Größe von der Gesamtmenge weggenommen werden. Das Verteilen hingegen lässt sich i.Allg. nicht direkt durch eine schriftliche Rechnungen darstellen, und man ist auf die Interpretation im Sinne des Aufteilens angewiesen (s. Verteilen) weshalb auch hier die schriftliche Rechnung durch die Subtraktion erfolgt. Wir wollen dies an ein paar Beispielaufgaben demonstrieren:
Der Inhalt einer 1,5-Liter-Getränkeflasche wird in Becher von 1/3 Liter umgefüllt. Wie viele Becher kann man füllen?Die entsprechende Rechnung lautet: 1
L.
÷ L. = ? D.h. wie oft kann man von 1 subtrahieren?|
1 L.
3 · L.
|
= | L. |
(3 Becher gefüllt; Rest 1/2 Liter) |
| L.
L.
|
= |  L. |
(1 weiterer Becher gefüllt; Rest 1/6 Liter) |
Darüber hinaus kann man hier leicht sehen, dass der Rest (1/6 Liter) einen Becher (1/3 Liter) zur Hälfte füllt, denn es ist 1/2 von 1/3 Liter = 1/6 Liter. Deshalb können wir das Ergebnis auch so formulieren:
⇒ 1
1
Wir können 4 Becher ganz füllen und einen zur Hälfte.
I. Allg. ist der letzte Schritt nicht so einfach wie in diesem Beispiel. Wäre der Rest etwa 1/5 ist (statt 1/6), dann müssten wir nach einem Bruch p/q suchen, so dass p/q von 1/3 = 1/5 ist, weshalb wir in einem solchen Fall die Rest-Schreibweise zunächst favorisieren.
Prinzipiell ist die Aufgabe p/q von 1/3 = 1/5 lösbar, wenn das Verfahren zur Multiplikation zweier Brüche bekannt ist: p/q · 1/3 = 1/5 und 1/5 = 3/15 ⇒ p/q = 3/5.
Petra erhält in 2Wir denken uns 2 ganze Portionen und eine halbe und verteilen das Geld:
Petra erhält also pro Monat 28 .
Die Lösung der folgenden Aufgabe führt bereits in die Nähe der üblichen Formel für die Division von Brüchen:
Timo erhält für 2/3 eines Monats 70 Taschengeld. Wie viel bekommt er im gesamten Monat?Wir denken uns 2/3 eines Monats und verteilen die 70 darauf:
Timo erhält in 1/3 eines Monats 35 , also bekommt er in einem Monat insgesamt 3·35 = 105 . (Er hat reiche Eltern!)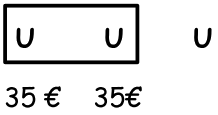
Die Aufgabenstellung entspricht einer der Grundaufgaben bei der Einführung von Brüchen: 2/3 von = 70 . Insbesondere sehen wir an der obigen Rechnung: Zur Bestimmung der Bezugszahl wird die zu verteilende Menge von 70 zuerst durch 2 dividiert und dann mit 3 multipliziert, was letztlich die Division 70 : 2/3 ausdrückt.
Übungsaufgaben:
