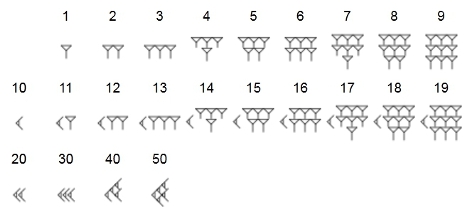
 |
http://www.wazimmer.de/matheKlasse5B_material-Dateien/Babylonische_Zahlen.pdfWeitere Links:
 sei
sei
 (in moderner Notation: 2;27² = 6;9).
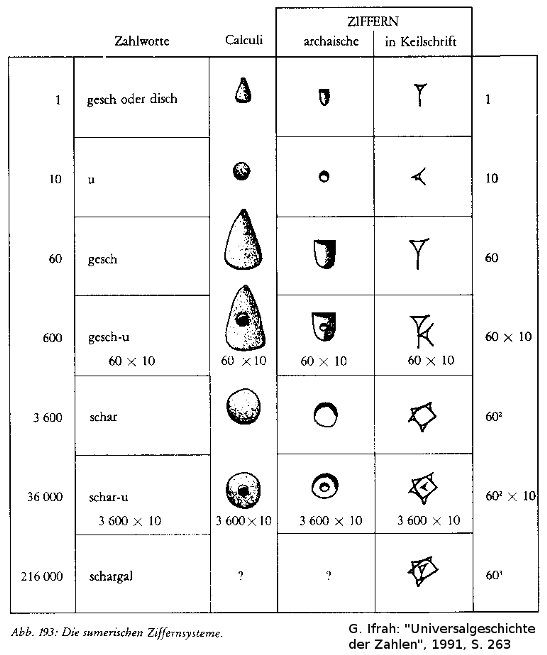
(in moderner Notation: 2;27² = 6;9).Im weiteren Verlauf der Geschichte wurden solche Zählsteinchen ersetzt durch entsprechende bildliche Darstellungen auf Lehmtafeln. Und aus letzteren entstand die o.g. Keilschrift. Im Unterschied zu dieser Keilschrift bildeten die Zählsteine und auch die darauf bezogenen Schreibsymbole aber kein Stellenwertsystem sondern nur ein Additionssystem wie etwa die römischen Zahlen.
 |
 |
 |
 |
|
|
(⇒ Päsentation als pdf-Datei) |
|
Unser Interesse an der Zahlschrift der Römer ist nicht nur historischer Art. Wegen ihrer Verwendung auf Urkunden und Gebäuden sowie gelegentlich bis heute im Alltag (Uhren-Ziffernblatt, Seitenzahlen etc.) ist diese Zahlschrift fester Bestandteil des Unterrichts in der Primarstufe. Dort gelten folgende Bildungsregeln:
Unabhängig von den jeweiligen Bildungsregeln ist die römische Zahlschrift ein Additionssystem, obgleich der Wert mancher Zahlen durch Subtraktion ermittelt wird. Denn Mit „Addition“ ist hier gemeint, dass nur die „Grundrechenarten erster Stufe“ (Addition, Subtraktion) gebraucht werden, im Unterschied zu den Stellenwertsystemen, die auch die Multiplikation und Potenzbildung benötigen (Grundrechenarten zweiter und dritter Stufe).
Zwei Missverständnisse:
|
 |
|
Die Inka verwendeten bis ins 17. Jh. eine sonderbare Zahlschrift: Sie formten auf Schnüren in regelmäßigen Abständen Knoten. Jede solche Knotenschnur stellte eine Zahl im dekadischen Stellenwertsystem dar. Wurde die Summe mehrerer Zahlen gebildet, so verband man die entsprechenden Schnüre durch eine weitere Schnur, auf der die Summe dargestellt war. Diese Knotenschrift heißt Quipu. Sie diente der Buchhaltung und hatte den Vorteil, dass nicht nur Ergebnisse sondern auch zugrunde liegende Daten und Rechnungen archiviert wurden. |
Unser Ziffern von 1 bis 9 gehen zurück auf die alte indische Brahmi-Schrift: 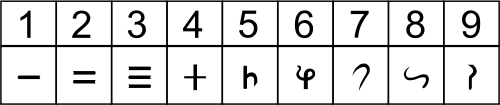
Aber erst seit dem 8. Jh. n.Chr. ist die Verwendung dieser Ziffern als Stellenwertsytem bezeugt – zusammen mit einem Kreis oder Punkt als Ziffer Null. Der älteste bisher bekannte Nachweis der Verwendung speziell eines solchen Zeichens für Null in einer Stellenwertzahl ist eine Inschrift in Kambodscha aus dem Jahr 683 (K. 127), wo das Jahr 605 angegeben ist (= 683/684 nach unserer Zeitrechnung).
In dem großen arabischen Reich, das nach dem Tod Mohammeds entstanden war, wurde das indische Zahlensystem schnell aufgenommen und verbreitete sich rasch. In dieser Kultur war allgemein das Interesse an Philosophie, Mathematik und Astronomie sehr groß, und wir verdanken heute unsere Kenntnisse der antiken Schriften größtenteils der Überlieferung durch die damalige arabische Kultur. Unsere Wörter „Algebra“ und Algorithmus“ z.B. zeugen noch von diesem Einfluss.
Erst ab dem 12. Jh. übernahm man auch in Europa das indische Zahlensystem, vermittelt durch die Araber. Von herausragender Bedeutung war dabei Leonardo von Pisa (ca. 1170 – ca. 1250) mit seinem Buch „Liber Abaci“.
Zahlen in einem Stellenwertsystem sind typischerweise Folgen von Ziffern, die je nach ihrer Position innerhalb der Folge unterschiedlich gewichtet werden, indem man sie mit dem Wert ihrer jeweiligen Stelle multipliziert. So wird z.B. die Ziffer 1 in 123 anders gewichtet als in 321. Und das gilt für alle Ziffern und Zahlen eines Stellenwertsystems. Dadurch ist es möglich, mit einem begrenzten Vorrat an Ziffern jede gewünschte natürliche Zahle darzustellen. Dagegen werden in additiven Zahlensystemen wie der römischen oder der ägyptischen Zahlenschrift für größere Zahlen immer weitere Zeichen oder Schreibweisen benötigt. Zwar kann in der römischen Zahlenschrift das Zeichen I je nach Positionierung bezüglich V oder X für +1 oder -1 stehen, aber für 10, 100 und 1000 etc. werden doch weitere Zeichen benötigt.
Allgemein können wir Stellenwertsysteme zu einer Basis b wie folgt beschreiben:
Die zweistellige Ziffernfolge 10 hat stets den Wert der Basis b, da 10b = 1·b1 + 0·b0 ist. Bei Stellenwertsystemen mit Basen b>10 werden mehr Ziffern benötigt als beim Dezimalsystem. In diesen Fällen werden heutzutage oft Buchstaben des Alphabets hinzugenommen (Hexadezimalsystem: 0, 1, 2, ..., 9, A, B, C, D, E, F). Oder die Ziffern, deren Wert 9 übersteigt, werden als eingeklammerte Zahlen des Dezimalsystems notiert (wieder Hexadezimalsystem: 0, 1, 2, ..., 9, (10), (11), (12), (13), (14), (15)). In leicht abgewandelter Form findet sich diese Schreibweise im 60er-System, z.B. bei Zeitangaben; statt Klammern um die Ziffern zu setzen werden diese durch Trennzeichen (wie Doppelpunkt oder Semikolon) voneinander abgesetzt: 23;45 = 23·601 + 45·600.
Die obige Definition lässt sich weiter verallgemeinern, indem man auch die Basis b in Abhängigkeit von der Position der Ziffern variiert. Dies trifft auf die Zahlen der Maya zu, die an der dritten Stelle nicht mit 202 sondern mit 20·18 gewichtet werden. Auch die uns geläufigen Zeitangaben in Stunden, Minuten und Sekunden bilden ein solches Stellenwertsystem nämlich mit den abwechselnden Basiszahlen 10 und 6; dazu später mehr.
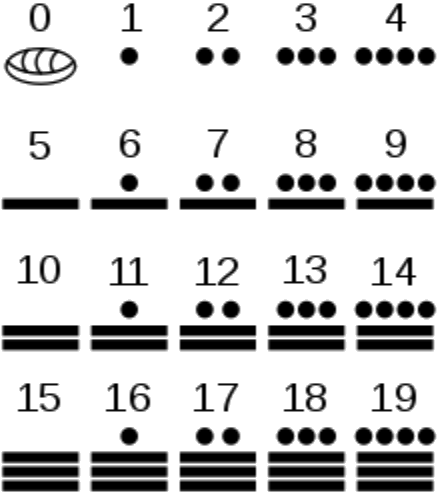
Im Unterschied zur römischen oder ägyptischen Zahlenschrift erfüllt das Zahlensystem der Maya und auch das mesopotamische 60er-System, die geforderten Kriterien für ein Stellenwertsystem. Die Zahlen der Maya von 0 bis 19 sind die Ziffern ihres Stellenwertsystems, dessen Basis b=20 ist – wenn man von der Abweichung an der 3. Stelle absieht. Entsprechend bilden in der mesopotamischen Keilschrift die Zahlen von 1 bis 59 zusammen mit dem Zeichen für die leere Stelle die Ziffern eines Stellenwertsystems zur Basis 60.
Bemerkung: Üblicherweise werden die indisch-arabischen Ziffern und Ziffernfolgen des herkömmlichen Zehnersystems nicht als natürliche Zahlen bezeichnet sondern als Zahldarstellungen. Doch wegen des Standardcharakters dieser Darstellung und wegen ihrer eineindeutigen Beziehung zu den natürlichen Zahlen, werden sie i. Allg. selbst wie natürliche Zahlen verwendet (z.B. „die Zahl 1“).
Da dies keine mathematischen Probleme bereitet, sondern vielmehr zur Vereinfachung der Ausdrucksweise beiträgt, wollen wir allgemein jede Zahldarstellung eine Zahl nennen (man spricht ja z.B. auch nicht von römischen Zahldarstellungen sondern von römischen Zahlen). Hinfällig wäre damit auch die Unterscheidung zwischen Ziffer und Zahl oder Ziffernwert.