
Nach: „Clock Arithmetic: A Mathematical System“ in: Musser/Burger/Peterson: „Mathematics for Elementary Teachers“, Intern. Student Version, 9. Ed., 2011
Angenommen wir hätten eine herkömmliche Analoguhr, die zehn Uhr anzeigt. Wir wüssten aber, dass diese Uhr vor genau elf Stunden stehengeblieben ist. Was müsste die Uhr also korrekterweise anzeigen? – Nun, wir könnten rechnen: 10 Uhr + 11 Stdn. ergibt 21 Uhr; das ist 9 Uhr. Wobei wir für letzteres eigentlich von 21 Uhr noch 12 Stdn. abziehen mussten. Wir könnten aber auch so rechnen: 10 Uhr – 1 Stdn. ergibt ebenfalls 9 Uhr. Dieser Rechenweg ist typisch für eine zyklische Arithmetik, wie wir sie vom Rechnen mit Uhrzeiten her kennen. Statt 11 Stunden zu addieren können wir 1 Stunde subtrahieren – und umgekehrt – und gelangen zur gleichen Uhrzeit.
Drehen wir den Stundenzeiger um 12 Stdn. vor oder zurück, dann ist er wieder in derselben Position wie zuvor. Eine Veränderung um 13 Stdn. hat dasselbe Ergebnis wie eine um nur 1 Stdn. usw. Wir brauchen deshalb bezüglich Addition und Subtraktion nur 12 Operationen zu unterscheiden, solange wir uns auf volle Stunden beschränken: +0, +1, +2, +3, …, +11. (Dazu gleichwertig ist: -5, -4, …, -1, ±0, +1, +2, …, +6.) Das Rechnen mit diesen Operationen weist einige sehr interessante Eigenschaften auf, die wir im Folgenden betrachten wollen. Wir wählen dazu jedoch ein anderes Modell als die 12-Stunden-Uhr: Wir nehmen eine fiktive 5-Stunden-Uhr, weil die Anzahl der Operationen daran überschaubarer ist. Diese sind: +0, +1, +2, +3, +4.
Führen wir zwei solche Operationen nacheinander aus, z.B. +1 und +2, drehen wir also den Stundenzeiger an der 5-Stunden-Uhr erst um 1 Stunde weiter und dann um 2, dann haben wir ihn effektiv um 3 Stunden weitergedreht – gleichgültig auf welcher Position er stand. Wir schreiben dafür 1⊕2=3 mit dem Zeichen ⊕, weil – wie wir gleich sehen werden – sich diese Addition am Zifferblatt der Uhr von der gewöhnlichen Addition unterscheidet. Drehen wir nämlich erst um 1 und dann um 4 Stunden weiter, so steht der Zeiger wieder dort wo er war, weshalb gilt: 1⊕4=0. Insgesamt ergibt sich folgende „1⊕1-Tafel“:
Wohlgemerkt: Wir addieren hier nicht Uhrzeiten! Es sind Drehungen des Stundenzeigers (also Winkel), die wir addieren.

Die Menge {0, 1, 2, 3, 4}, wir nennen sie C5, mit der Addition ⊕ am Zifferblatt der Uhr als Verknüpfung hat folgende Eigenschaften:
Die Subtraktion auf C5 können wir als Rückwärtsbewegung des Stundenzeigers auffassen oder als Addition des jeweiligen inversen Elements. Demnach ist z.B. 4![]() 1=4⊕(-1)=4⊕4=3 und 1
1=4⊕(-1)=4⊕4=3 und 1![]() 2=1⊕(-2)=1⊕3=4.
2=1⊕(-2)=1⊕3=4.
All diese Eigenschaften gelten nicht nur für die Menge C5 sondern für jede Menge Cn mit der entsprechenden Addition ⊕ wobei n eine beliebige natürliche Zahl ab 1 sein kann, n∈{1,2,3,…}.
Übungsaufgabe: Berechnen Sie die folgenden Ausdrücke in der jeweiligen Gruppe (Cn,⊕).
a) 6⊕8 (C12) b) 4⊕4 (C5) c) 7⊕4 (C9)
d) 82 (C12) e) 1
4 (C5) f) 2
5 (C7)
Weiterhin lässt sich auf jeder Gruppe (Cn,⊕) auch die Multiplikation einführen. Wir machen das ebenso wie bei den natürlichen Zahlen als wiederholte Addition und sagen n⊗m = m⊕m⊕…⊕m (d.h. n-mal m). Damit erhalten wir für C5 die folgende 1⊗1-Tafel:
Wie können schnell nachprüfen, dass C5 auch bezüglich der Multiplikation ⊗ eine kommutative Gruppe ist (ohne 0). Doch gilt diese Eigenschaft nicht für alle Cn, sondern nur wenn n eine Primzahl ist. Dazu ein kleines Beispiel an der herkömmlichen 12-Stunden-Uhr: Die Vielfachen von 3 in C12 sind: 0, 3, 6 und 9. Es gibt offensichtlich kein multiplikatives Inverses von 3 in C12, also keine Zahl x, so dass 3⊗x=1 ergibt. In C5 dagegen gibt es das: 3⊗2=1, weshalb in C5 gilt: 3-1 (= ¹⁄₃) =2. Es kommt aber noch mysteriöser: In der Schule lernt man, dass ein Produkt zweier Zahlen nur dann null ist, wenn mindestens einer der Faktoren null ist. In C12 stimmt das nicht. Es gilt dort nämlich 3⊗4=0. Solche Zahlen, deren Produkt null ergibt, obwohl beide nicht null sind, heißen Nullteiler. Dahingegen können wir in Gruppen Cn, bei denen n eine Primzahl ist, rechnen wie in den rationalen Zahlen (ganz Zahlen und Brüche), auch wenn die Resultate ungewohnt erscheinen mögen. Welche Nullstellen hat z.B. x2+1 in C5 (das ist dort x⊗x ⊕1)? Sie können es ausprobieren, weil C5 ja nur aus 5 Elementen besteht. Am einfachsten schauen Sie in der Diagonale der 1⊗1-Tafel nach. Dort findet sich: 22=4 und 32=4, was wegen 4⊕1=0 die Lösungen 2 und 3 ergibt.
Übungsaufgabe: Berechnen Sie, falls überhaupt möglich, die folgenden Terme.
Unter der Division ![]() verstehen wir die Multiplikation mit dem multiplikativen Inversen, also x
verstehen wir die Multiplikation mit dem multiplikativen Inversen, also x![]() y=x⊗(y-1), wobei y⊗(y-1)=1.
y=x⊗(y-1), wobei y⊗(y-1)=1.
a) 5⊗7 (C12) b) 4⊗2 (C5) c) 6⊗5 (C8)
d) 13 (C7) e) 2
5 (C7) f) 2
6 (C12)
Dreht man den Stundenzeiger auf dem Zifferblatt einer herkömmlichen Analoguhr um 13 Stunden weiter, hat er die gleiche Position als hätte man ihn nur um 1 Stunde weitergedreht. Das Gleiche gilt für 25 Stunden, 37 Stunden usw. Diese Zahlen lassen sich der Reihe nach durch den Term 1+n·12 berechnen (n=0,1,2,…). Beliebige zwei Zahlen davon unterscheiden sich folglich nur durch ein Vielfaches von 12: (1+n·12) – (1+m·12)=(n – m)·12. Für diesen Zusammenhang gibt es einen eigenen Begriff:
Kongruenz modulo kSo ist z.B. 1≡13 mod 12 und ebenso 13≡37 mod 12.
Sind a, b und k ganze Zahlen, so dass k>1 ist und dass für irgendeine ganze Zahl t gilt: a – b = t·k (d.h. k ist ein Teiler von a – b),
dann sagt man a ist kongruent b modulo k, geschrieben: a ≡ b mod k.
Übungsaufgabe: Welche der folgenden Kongruenzen sind wahr? Begründen Sie Ihre Antwort.
a) 13 ≡ 7 mod 2 b) 5 ≡ 11 mod 6 c) -5 ≡ 14 mod 6 d) -7 ≡ -22 mod 5
Die Ähnlichkeit des Zeichens ≡ zum Gleichheitszeichen kommt nicht von ungefähr, wie wir an den folgenden Eigenschaften gleich sehen. Den Ausdruck modulo k lassen wir weg, weil sich alle Kongruenzen auf ein beliebiges aber doch festes k>1 beziehen:
¹⁄₇ = ¹⁴²⁸⁵⁷⁄₉₉₉₉₉₉ (= 0,142.857.142.857…)Und weil es keine kleinere Zahl als 6 mit dieser Eigenschaft gibt, ist das die Periodenlänge von ¹⁄₇ (im 10er-System). Wenn wir aber nur an der Periodenlänge interessiert sind, genügt es umgekehrt völlig, einen kleinsten Exponenten n zu finden, so dass 10n ≡ 1 mod 7 ist. Und dafür nutzen wir die obigen Eigenschaften:
⇔ 7·142.857 = 999.999, d.h.: 7·142.857 = 106 – 1
⇔ 106 ≡ 1 mod 7.
Übungsaufgabe: Bestimmen Sie in gleicher Weise die Periodenlänge von ¹⁄₁₇.
An welchem Wochentag hatten Sie im Jahr 2019 Geburtstag? War es ein Sonntag? Wenn ja: Dann war Ihr Geburtstag 2018 eindeutig an einem Samstag; das können wir mit Sicherheit sagen. Aber für das Jahr 2020 lässt sich dieser Wochentag nicht mehr so einfach bestimmen – jedenfalls nicht ohne weitere Informationen. Immerhin, soviel können wir doch mit Sicherheit sagen: Es ist ein Montag oder ein Dienstag. Welcher der beiden Wochentage es ist, hängt ganz davon ab, ob Ihr Geburtstag vor dem 1. März liegt (Januar, Februar) oder nicht (März, April, …, Dezember). Sie ahnen den Grund: 2020 ist ein Schaltjahr, und unmittelbar vor dem 1. März liegt der Schalttag 29. Februar. In gewöhnlichen Jahren verschiebt sich der Wochentag von einem Geburtstag zum nächsten um 1 Tag; liegt jedoch ein Schalttag dazwischen, dann sind es 2 Wochentage. Der Grund dafür ist einfach: Ein gewöhnliches Jahr – man nennt es auch Gemeinjahr – hat 365 Tage; das sind 52 Wochen und 1 Tag: 365 = 52·7 + 1. Wegen dieses einen Tages ändert sich der Wochentag von Geburtstag zu Geburtstag um 1 Tag; und um 2 Tage, wenn ein Schalttag dazu kommt. Bestünde jedes Jahr nur aus einer ganzen Anzahl von Wochen, wäre also die Anzahl der Tage ein Vielfaches von 7, dann hätten wir immer an denselben Wochentagen Geburtstag.
Beispielsweise war der 23. Januar der Geburtstag von David Hilbert (1862 – 1943). 2015 war das ein Freitag, 2014 ein Donnerstag, und 2016 ist es ein Samstag. Für 2017 müssen wir zwei Wochentage weiterzählen, weil zwischen dem 23. Januar 2016 und demselben Datum im Jahr darauf ein Schalttag liegt; das Datum fiel 2017 also auf einen Montag. Wir können diese Zählung fortsetzen und kommen damit zu folgender Tabelle für die Wochentage des 23. Januar in den angegebenen Jahren:
|
Wenn wir nun aber den Wochentag des 23. Januar 2065 also in 50 Jahren ausgehend von 2015 bestimmen wollen, dann sicher nicht so! Es geht in dem Fall nämlich schneller, indem wir die Verschiebung des Wochentags zunächst ohne Berücksichtigung der Schalttage berechnen und anschließend einfach die Schalttage addieren:
Der in der westlichen Kultur übliche und weltweit bekannte gregorianische Kalender gilt seit dem 15. Oktober 1582. Er löste den vorhergehenden julianischen Kalender ab, bei dem strikt alle 4 Jahre ein Schaltjahr stattzufinden hatte (Jahreszahlen, die Vielfachen von 4 sind). Im gregorianischen Kalender sollen dagegen in 400 Jahren 3 Schalttage weniger vorkommen. Man hat sie auf die Jahre gelegt, die Vielfache von 100 sind aber keine Vielfache von 400. Deshalb waren 1700, 1800 und 1900 keine Schaltjahre, 1600 und 2000 aber doch. (Zu Details siehe: „Gregorianischer Kalender“, Wikipedia.)
Übungsaufgabe:
Auf welchen Wochentag fällt der 23. Januar 2115, also in 100 Jahren ausgehend von 2015? Und in 400 Jahren?
Nach 400 Jahren wiederholt sich im gregorianische Kalender die Zuordnung von Datum zu Wochentag, so dass wir 2015 den gleichen Kalender verwenden könnten wie 1615 (das gilt nicht für alle Kalenderdaten wie z.B. Ostern, das auch mit den Mondphasen zusammenhängt). Denn 400 Jahre sind eine ganze Anzahl an Wochen – es gibt keine restliche Tage. Auf dieser Periodizität beruhen ewige Kalender wie der folgende in Tabellenform:
(⇒Anklicken zum Vergrößern)
Quelle: „Ewiger Kalender gregorianisch mit Jahrhunderten“ von LenderCarl - Eigenes Werk.
Lizenziert unter CC BY-SA 3.0 über Wikimedia Commons.
Übungsaufgabe: Die Doomsdaymethode des Mathematikers John Horton Conway nutzt zur Berechnung des Wochentags im Kopf, dass die folgenden Kalendertage immer auf denselben Wochentag fallen: 4.4., 6.6., 8.8., 10.10., 12.12. Es ist derselbe Wochentag wie der des letzten Tags im Februar – egal ob Schaltjahr oder nicht. Und dieser Wochentag eines bestimmten Jahres wird aus der Kenntnis des entsprechenden Tages in einem beliebigen Jahr ermittelt, z.B. war der 29. Februar 2000 ein Dienstag.
a) Bestimmen Sie rechnerisch den Wochentag des letzten Februartags in den Jahren 1600, 1700, 1800 und 1900.
b) Johann Wolfgang von Goethe ist am 28. August 1749 geboren. Bestimmen Sie den Wochentag nach der Doomsdaymethode.
Überprüfen Sie Ihre Ergebnisse mit dem o.g. ewigen Kalender.
Lesetipps:
Als Intervall bezeichnet man in der Musik den Tonhöhenabstand zweier Töne eines Tonsystems. Das wichtigste Intervall jedes Tonsystems überhaupt ist die Oktave. Töne, die sich um genau eine oder mehrere Oktaven in ihrer Höhe unterscheiden, werden von uns als ‚sehr ähnlich‘ wahrgenommen. Aus diesem Grund haben sie auch gleiche Namen erhalten. Zwei solche Töne klingen zwar sehr ähnlich, aber sie sind selbstverständlich nicht gleich, da sie sich in der Tonhöhe unterscheiden und damit unterschiedliche Schwingungsfrequenzen haben. Z.B. hat der Standard-Kammerton a eine Frequenz von 440 Hz; d.h. ein Lautsprecher oder die Saite eines Musikinstruments, das diesen Ton erzeugt, führt 440 Schwingungen pro Sekunde aus. Das nächst höhere a hat dann eine Frequenz von 880 Hz und das a darunter eine von 220 Hz. Allgemein hat der um eine Oktave höhere Ton immer die doppelte Frequenz. Beträgt der Unterschied zwei Oktaven, dann ist die Frequenz also viermal so groß. Nebenbei sehen wir an diesem Beispiel auch, dass sich Intervall- und Frequenzarithmetik unterscheiden: doppeltes Intervall heißt nicht doppelte Frequenz! Wir kommen später noch einmal darauf zurück. Im Moment ist für uns nur wichtig, dass wir ein Tonsystem verwenden können, in dem die Oktave in 12 gleich große Halbtonschritte unterteilt ist: die 12-stufig gleichtemperierte Stimmung. Es ist das dominierende Tonsystem der westlichen Musik.
Der Begriff Oktave (von lateinisch octava ‚die achte‘) leitet sich ab von der 7-schrittigen Tonleiter c-d-e-f-g-a-h-c, bei der von acht aufeinanderfolgenden Tönen stets der 1. und der 8. eine Oktave bilden. Eine solche inklusive Zählung war in der Antike auch bei kalendarischen Angaben durchaus üblich und führte nach der Einführung des Julianischen Kalenders etwa zu dem Fehler, dass alle drei statt vier Jahre ein Schaltjahr stattfand, weil man das letzte Schaltjahr mitzählte: 1.-2.-3.-4.. Bemerkenswert ist diese Zählweise, weil auch Kinder sie zur Addition kleiner Zahlen oftmals falsch einsetzen, z.B. 5+3: 5,6,7 also 5+3=7.
Übungsaufgabe:
Das Gehör eines jungen Menschen kann Töne von ca. 20 Hz bis 20 kHz wahrnehmen. Wie viele Oktaven sind das?
Wegen der gleichmäßigen Unterteilung der Oktave können wir darin 13 Intervalle unterscheiden: Von 0 Halbtonschritten Abstand zweier Tonhöhen (also gleicher Tonhöhe) bis 12 Halbtonschritten Abstand, was eine Oktave ist. Wir bezeichnen Sie mit I0, I1,…, I12. Herkömmliche Bezeichnungen dafür sind:
|
In + Im = In+m(Wie schon bei den obigen Beispielen verstehen wir unter der Summe zweier Intervalle Folgendes: Sind x, y und z drei aufsteigende Tonhöhen, von denen x und y das Intervall In sowie y und z das Intervall Im bilden, dann ist In+m das Intervall zwischen x und z.)
Es gibt gewiss gute innermusikalische Gründe, an den herkömmlichen Intervallbezeichnungen festzuhalten. Mehr noch: Musiker unterscheiden sogar weitere Bezeichnungen innerhalb einer Oktave. So kann eine übermäßige Quarte etwa als Tritonus bezeichnet werden aber nicht als verminderte Quinte, obwohl es sich rein akustisch in der gleichtemperierten Stimmung um exakt dasselbe Intervall handelt. Ein Unterschied liegt aber möglicherweise im Kontext. Denn Intervalle sind in größere Musikstücke eingebettet, wo ihnen andere Intervalle vorausgehen bzw. nachfolgen.
Wir sind hier jedoch nur an einem bestimmten arithmetischen Aspekt der Intervall-Lehre interessiert und wollen diesen möglichst prägnant herausstellen. Dass er überhaupt existiert, finden wir alleine schon sehr bemerkenswert.
Wenn wir nur solche Tonhöhen voneinander unterscheiden, die nicht durch eine oder mehrere Oktaven getrennt sind, dann bekommt unser Tonsystem eine zyklische Struktur. Ausgehend z.B. von c gelangen wir nach 12 Halbtonschritten (I1) wieder zu einem c, das wir jedoch zum vorhergehenden wegen des Oktavabstands (I12) als äquivalent ansehen wollen. Salopp gesagt fassen wir also alle c's (alle c genannten Tonhöhen) zu einer Tonhöhenklasse zusammen; ebenso alle cis genannten Tonhöhen zu einer weiteren Klasse etc.
Dieser Übergang vom linearen Tonhöhensystem zur zyklischen Tonleiter lässt sich mathematisch als Äquivalenzklassenbildung modulo Oktave beschreiben. Zu diesem Zweck sehen wir zwei Tonhöhen x und y genau dann als äquivalent an, in Zeichen: x~y, wenn ihr Abstand genau n Oktaven beträgt (n=1,2,3…). Damit lässt sich das gesamte Tonhöhensystem in Klassen äquivalenter Tonhöhen einteilen, den Tonhöhenklassen. Ist also x eine Tonhöhe, dann beinhaltet die Tonhöhenklasse x* außer x auch alle darüber und darunter liegenden Oktaven von x. Deshalb gelangt man ausgehend von x* nach 12 Halbtonschritten wieder zu x* zurück. Folglich bilden diese Tonhöhenklassen in Halbtonschritten angeordnet eine zyklische Tonleiter, und die an der Tonleiter-Uhr notierten Tonhöhen sind jeweils Repräsentanten dieser Äquivalenzklassen, welche alle in einer Oktave liegen.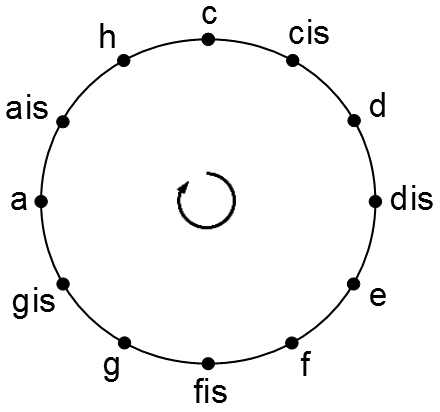
In Bezug auf die zyklische Tonleiter hat das Intervall I12 (die Oktave) die gleiche Bedeutung wie I0 (die Prime). Denn man gelangt nach 12 Halbtonschritten (I1) zur gleichen Tonhöhenklasse zurück, von der man ausging; der Abstand der beiden Klassen ist 0. Wir können daher ähnlich wie bei den Tonhöhen auch bei den Intervallen eine Äquivalenz sehen. Denn Intervalle, die sich nur um eine oder mehrere Oktaven unterscheiden, geben auf der zyklischen Tonleiter denselben Abstand wieder (sie sind äquivalent modulo Oktave). Deswegen genügt es, die Überlegungen dazu auf die Intervalle I0 bis I11 zu beschränken. Sie repräsentieren nämlich alle möglichen Abstände auf dieser Tonleiter.
Sind zwei Intervalle In und Im äquivalent, dann schreiben wir In ~ Im. Sie sind dann entweder gleich, oder sie unterscheiden sich nur um eine oder mehrere Oktaven. Damit notieren wir für die Beziehung von I12 zu I0 bezüglich der zyklischen Tonleiter kurz: I12 ~ I0.
Wenn wir zwei dieser Intervalle In, Im mit m, n ∈ {0,…,11} addieren, zeigen sich bemerkenswerte Eigenschaften:
Sind m, n ∈ {0,…,11}, dann ist In + Im ~ Ir, wobei r der Rest bei der Division (m+n)÷12 ist.Man sagt, die Menge der Intervalle I0 bis I11 ist bezüglich dieser Addition abgeschlossen.
Ist n ∈ {0,…,11} dann gilt In + I12-n ~ I0I12-n heißt Komplementärintervall zu In und umgekehrt.
Übungsaufgabe: Ein Dur-Akkord besteht aus einem Grundton sowie der Quinte (I7) und der großen Terz (I4) darauf. Ist t der Grundton, und bezeichnen wir mit I4(t) bzw. I7(t) die Tonhöhen, die im Abstand I4 bzw. I7 nach oben folgen, dann können wir den entsprechenden Dur-Akkord auch wie folgt notieren: (t, I4(t), I7(t)). Bestimmen Sie so die Dur-Akkorde zu den Grundtönen c, d und e.
Wesentlich für einen Ton ist nicht nur seine Frequenz sondern auch seine Klangfarbe, und die wird durch Obertöne bestimmt. Denn die Schwingungen, die einen Ton der Frequenz f bilden, haben zwar i.Allg. keine reine Sinusform, aber sie lassen sich als Überlagerung solcher Sinusschwingungen der Frequenzen f, 2f, 3f, … interpretieren, und als Obertöne bezeichnet man die mit den Frequenzen 2f, 3f, … Daraus folgt nun, dass in der Obertonreihe eines jeden Tons mit Frequenz f auch seine Oktaven enthalten sind: 2f, 4f,... Das ist der Grund für die Ähnlichkeit von Oktaven. (Die Frequenzen der Obertöne von natürlich erzeugten Tönen weichen von den idealen Werten oft etwas ab, was bei der Stimmung der Instrumente zu berücksichtigen ist; Stichwort: Streckung oder Spreizung.)
Wenn man weiß, dass das Frequenzverhältnis eines Tons zu seiner nächst höheren Oktave 1:2 ist, stellt sich die Frage, welche Frequenzverhältnisse andere Intervalle haben. Wir wollen zunächst das Verhältnis des Halbtonschritts also des Intervalls I1 bestimmen: In der gleichstufigen Stimmung eines Tonsystems besteht die Vorgabe, dass alle Frequenzverhältnisse zwischen benachbarten Tonhöhen gleich sein sollen. Bezeichnen wir mit f0 die Frequenz eines Tons dieses Systems (z.B. c) und mit f1, f2, …, f12 die Frequenzen der darauf folgenden 12 Tonhöhen (einschließliche der Oktave dieses Tons), dann soll gelten: x·f0=f1, x·f1=f2, …, x·f11=f12. Daraus folgt, dass x12·f0=f12 gelten soll. Wegen des Oktav-Verhältnisses zwischen f0 und f12 soll aber auch 2·f0=f12 gelten. Dann muss x12=2 sein oder x=21/12 (= ![]() ); das ist eine irrationale Zahl ≈1,0594630943593. Also ist die Frequenz eines jeden Tons ca. 5,9% höher als die des unmittelbar in der Höhe vorausgehenden. Wir wollen diese Zahl
); das ist eine irrationale Zahl ≈1,0594630943593. Also ist die Frequenz eines jeden Tons ca. 5,9% höher als die des unmittelbar in der Höhe vorausgehenden. Wir wollen diese Zahl ![]() im Weiteren mit dem Buchstaben q abkürzen.
im Weiteren mit dem Buchstaben q abkürzen.
Nun sind wir soweit, die Frequenzverhältnisse aller Intervalle der gleichstufigen Stimmung anzugeben. Bilden nämliche zwei Tonhöhen x und y aufsteigend ein Intervall In, dann ist y um n Halbtonschritte höher als x, so dass für die Frequenz fy gilt: fy=fx·qn.
Damit hat jedes Intervall In das Frequenzverhältnis (fy/fx): qnSind weiter x, y und z drei aufsteigende Tonhöhen mit den Intervallen In zwischen x und y sowie Im zwischen y und z, dann sind deren Frequenzverhältnisse qn bzw. qm. Und das Frequenzverhältnis fz/fx der Tonhöhen x und z, was dem Intervall In+m entspricht, ist =qn+m. Deshalb gilt:
Die Summe zweier Intervalle In + Im hat das Frequenzverhältnis qn·qm (=qn+m).Also entspricht die Addition von Intervallen der Multiplikation der jeweiligen Frequenzverhältnisse.
Warum unterteilt man den Frequenzbereich der Oktave nicht additiv in 12 Halbtonschritte: x+f0=f1, x+f1=f2, …, x+f11=f12? Abgesehen von klanglichen oder harmonischen Gesichtspunkten, ließe sich das nur für eine bestimmte Oktave (mit festen Frequenzen f0 und f12) so festlegen. Denn der Frequenzbereich der nächst höhere Oktave (von f12 bis f24) ist doppelt so groß (f24=2·f12=4·f0) und bestünde somit aus doppelt so großen Halbtonschritten.
Das irrationale Frequenzverhältnis benachbarter Töne der gleichstufigen Stimmung hat zur Folge, dass die Obertöne aller 12 Töne (ohne Oktave) verschieden sind. Nun ist die Gleichstufigkeit eine relativ neue Erscheinung in der Musik mit Anfängen im 16. Jhd. In der Antike und im Mittelalter praktizierte man dagegen eine reine Stimmung, bei der die Frequenzverhältnisse rational waren also Brüchen entsprachen, so dass die Töne in einigen Obertönen übereinstimmten.
Das nächst wichtige Frequenzverhältnis nach der Oktave ist in einer reinen Stimmung die Quinte. Z.B. ist g in der 7-schrittigen Tonleiter c-d-e-f-g-a-h-c der 5. Ton von c aus, es ist die Quinte zu c, und die Frequenzen der beiden Töne haben in der reinen Stimmung das Verhältnis fc : fg = 2 : 3, so dass die Frequenz von g das 1,5-fache der Frequenz von c ist. Nun hat der erste Oberton immer die doppelte Frequenz des Grundtons, sie bilden eine Oktave. Die Frequenz des 1. Obertons von g ist also 2⋅(1,5⋅fc), das ist die 3-fache Frequenz von c und damit die Frequenz des 2. Obertons von c. Das gilt allgemein: Ist y die reine Quinte zu x, dann hat der 1. Oberton von y die die gleiche Frequenz wie der 2. Oberton von x.
Musikalisch ausgedrückt ist der 1. Oberton die Oktave zum Grundton (doppelte Grundfrequenz). Der 2. Oberton hat die 3-fache Grundfrequenz also die 1,5-fache des 1. Obertons (1,5⋅2=3). Daher ist der 2. Oberton in der reinen Stimmung die Quinte zum 1. Oberton: Grundton → Oktave → Quinte. Von c ausgehend sind das c' und g' (c und g in der nächst höheren Oktave). Deshalb klingen Quinten harmonisch.
Die Quinte von c ist g, und c selbst ist die Quinte des nächst niedrigeren f: f→c→g. Wir sehen also: Zwei Quintenschritte führen zum gleichen Ergebnis wie ein Ganztonschritt und eine Oktave. (Zwei Halbtonschritte sind ein Ganztonschritt.) Deshalb lässt sich die eben begonnene Quintenfolge einfach weiterführen: f→c→g→d→a→e→h. Von e nach f sowie von h nach c haben wir keine Ganzton- sondern Halbtonschritte, so dass nach e und h in der Quintenfolge fis und cis kommen: f→c→g→d→a→e→h→fis→cis→gis→dis→ais. Somit können wir alle 12 Tonhöhen der Tonleiter durch fortgesetzte Quintenbildung erzeugen, auch wenn sich die einzelnen Töne bei Verwendung des reinen Quintenverhältnisses 2:3 ein wenig von denen der gleichstufigen Tonleiter unterscheiden. Diese Art der Stimmung nur nach reinen Quinten heißt pythagoräische Stimmmung.
Allerdings führt die wiederholte Quintenbildung der pythagoräischen Stimmung nicht mehr zur Ausgangstonhöhe (bzw. deren Oktave) zurück. Der Quintenzirkel (s.u.) schließt sich in der pythagoräischen Stimmung nicht, es ist eine Quintenspirale. Nach dis und ais kommen nicht wieder f und c sondern zwei neue Tonhöhen, die etwas höher liegen als diese (aber niedriger als fis und cis). Das ist rechnerisch ganz offenkundig: Ist nämlich fx die Frequenz eines beliebigen Tons x, dann ist fx·(3/2)12 die Frequenz des Tons nach 12 Quintenschritten. Aber (3/2)12 ist nie und nimmer eine 2er-Potenz (2, 4, 8, usw.), was es jedoch sein müsste, um auch ein Oktavenverhältnis darzustellen, so dass sich der Kreis schließen kann. Wir können sogar genau sagen, wie viele Oktaven diese 12 Quinten bilden müssten. Zwei Quinten bilden eine Oktave und einen Ganztonschritt, weshalb 12 Quinten 6 Oktaven und 6 Ganztonschritte bilden sollten. Da 6 Ganztonschritte eine Oktave sind, sollten wir mit 12 Quinten genau 7 Oktaven erhalten. Es ist jedoch (3/2)12 ≠ 27. Das Verhältnis (3/2)12:27 ≈1,0136432647705078125 heißt Pythagoräisches Komma. Der neue Ton nach 12 Quinten hat also eine etwa 1,4% höhere Frequenz als der Ton nach 7 Oktaven. Durch Stimmung eines Instruments nach reinen Quinten erhält man daher keine 12-stufige Tonleiter. Instrumente, die in reinen Quinten gestimmt sind, erzeugen eine, die nicht rein ist: die Wolfsquinte.
Lesetipps: