| usw. |
Die Arithmetik ist schon seit der Antike fester Bestandteil akademischer Bildung (→Quadrivium). Euklid behandelt sie in den Büchern VII-IX seiner „Elemente“ (ca. 300 v.Chr.):
Die Sätze über gerade und ungerade Zahlen im Buch IX sind (wie etliche andere Sätze auch) wohl älter und stammen wahrscheinlich von den Pythagoreern. Doch leider ist von ihnen selbst nichts schriftlich überliefert, so dass die Urheberschaft spekulativ bleibt. Das ist auch deswegen sehr bedauerlich, weil man vermutet, dass die Beweise der arithmetischen Sätze bei ihnen anders waren – nicht so geometrisch verklausuliert. (Man tut von daher gut daran, sich zunächst eigene Gedanken über mögliche Begründungen zu machen, ehe man die Beweise aus den Elementen durchliest.) Die Definitionen der Begriffe „Zahl“, „gerade Zahl“ sowie „ungerade Zahl“ aus Buch VII und die ersten drei Sätze über diese Zahlen aus Buch IX lauten nach Euklid wie folgt:
- Teilbarkeit, Primzahlen, Euklidischer Algorithmus
- Quadrat-/Kubikzahl, geometrische Folgen
- Gerade und ungerade Zahlen, Unendlichkeit der Primzahlen, Summenformel für die geometrische Reihe, Formel für vollkommene Zahlen
(s. →R. Haller: „Euklides: Stoicheia“ (1884), →Euclid's Elements)
- Definition 2: Eine Zahl ist eine Vielheit, die aus Einheiten besteht.
- Definition 6: Eine gerade Zahl ist eine solche, die in zwei gleiche Teile zerlegbar ist.
- Definition 7: Eine ungerade Zahl ist eine solche, die nicht in zwei gleiche Teile zerlegbar ist, oder die sich um eine Einheit von einer geraden Zahl unterscheidet.
- Satz 21: Die Summe von beliebig vielen geraden Zahlen ist gerade. [→Beweis]
- Satz 22: Die Summe einer geraden Anzahl ungerader Zahlen ist gerade. [→Beweis]
- Satz 23: Die Summe einer ungeraden Anzahl ungerader Zahlen ist ungerade. [→Beweis]
Die Beweisführung bei Euklid erscheint mysteriös, um nicht zu sagen abwegig. Hatte er tatsächlich Strecken für Zahlen im Sinne? Ausgerechnet Strecken, die sich (in anderem Zusammenhang) beliebig teilen lassen?
Es scheint, als hätte man sich für Zahlen ursprünglich etwas ganz Anderes vorgestellt als Strecken, nämlich doppelreihige Punktmuster:
Damit jedenfalls wird die Beweisführung etwa zu Satz 21 unmittelbar einsichtig: „[…] Denn da AB, BC, CD, DE gerade sind, sind sie in zwei Teile teilbar, deshalb ist auch AE in zwei gleiche Teile teilbar. […]“
usw.
Quadratzahlen und binomische Formeln
Egal ob die Pythagoreer nun so dachten oder nicht, diese figurierten Zahlen, wie man sie nennt, sind außerordentlich inspirierend. Die Zahlen 4, 9, 16, 25, … z.B., die unschwer als Quadratzahlen zu erkennen sind, haben diese Bezeichnung, weil sich nur mit ihnen quadratische Punktmuster bilden lassen:
 |
 |
Und es ist ein Leichtes, an diesen Mustern Zusammenhänge zwischen den Zahlen zu erkennen. Wie kann man beispielsweise aus einem 2×2-Quadrat ein 3×3-Quadrat machen? Klar: Indem man 2 Punkte rechts hinzufügt, 2 oben und einen in der Ecke. Also ist 2×2 + 2 + 2 + 1 = 3×3. Allgemein: Wie kann man aus einem n×n-Quadrat ein (n+1)×(n+1)-Quadrat machen? Klar: Indem man n Punkte rechts hinzufügt, n oben und einen in der Ecke. Also ist n×n + n + n + 1 = (n+1)×(n+1) oder n² + 2n + 1 = (n+1)². |
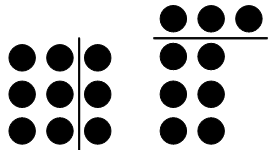 |
Nimmt man hingegen von dem 3×3-Quadrat eine Spalte seitlich weg und legt sie als Reihe oben auf, dann erhält man ein 2×4-Rechteck mit einem überschüssigen Punkt. Also ist 3×3 = 2×4 + 1, allgemein: n×n = (n−1)×(n+1) + 1. Das ist in der üblichen Notation: (n−1)(n+1) = n² − 1. |
Übungsaufgabe: Interpretieren Sie die folgenden Gleichungen an quadratischen Punktmustern.
Im 1×1 finden sich viele Bezüge zu den obigen Formeln rund um die Quadratzahlen. Betrachten wir etwa 5×5=25:
Dreieckszahlen und arithmetische Reihen
Führen Produkte der Form n×n zu quadratischen Punktmustern, so führen Summen der Form 1+2+3+…n zu dreieckigen Mustern und zu den sog. Dreieckszahlen 3, 6, 10, 15, … (d.h. 1+2, 1+2+3, 1+2+3+4, usw.).
 |
Einer Anekdote zufolge sollte C.F. Gauss als 9-jähriger Schüler die Zahlen von 1 bis 100 addieren. Er war nach wenigen Minuten fertig und präsentierte seinem verdutzten Lehrer das Ergebnis. Gauss hatte festgestellt, dass die erste und die letzte Zahl (1+100), die zweite und die vorletzte Zahl (2+99) usw. zusammen immer 101 ergeben, so dass die gesuchte Summe gleich 50×101 war. Möglicherweise war dem Lehrer die Besonderheit dieser Aufgabenstellung sehr wohl bewusst, auch wenn das in der Anekdote so nicht überliefert wird. Denn die Berechnung der Dreieckszahl 1+2+3+…+100 kommt bereits um 800 n.Chr. in der Aufgabensammlung des Alcuin als Aufgabe XLII vor. Dort geht es um eine Treppe mit 100 Stufen, auf denen Tauben sitzen. Eine Taube auf der ersten Stufe, 2 Tauben auf der zweiten usw. Zu berechnen ist die Gesamtzahl der Tauben. Alcuin schlägt dazu folgenden Lösungsweg vor: 100+(99+1)+(98+2)+…+(51+49)+50. |
|
(⇒ Präsentation als pdf-Datei) |
Übungsaufgabe:
Berechnen Sie die Summe der ersten zehn geraden Zahlen: 2+4+6+8+…+20.
Entwickeln und begründen Sie eine allgemeine Formel für die Summe von n geraden Zahlen (ab 2): 2+4+…+2(n−1)+2n.
(→ Antwort)
Hier ist ein aktuelles Beispiel zur Verwendung von Dreieckszahlen im 2. Schuljahr: „Das Zahlenbuch 2“
Zahlenfolgen wie die geraden Zahlen oder die Vielfachen von drei usw. nennt man arithmetische Folgen. Die Differenz aufeinanderfolgender Zahlen einer arithmetischen Folge ist konstant. Insofern bilden auch die natürlichen Zahlen 1,2,3,… eine solche Folge. Weitere Beispiele sind etwa die ungeraden Zahlen 1,3,5,… oder die Zahlen 1,4,7,… (allg. 3n+1).
Die Summe einer arithmetischen Zahlenfolge heißt arithmetische Reihe. Im Fall der natürlichen Zahlen bilden die Dreieckszahlen die zugehörige arithmetische Reihe: 1, 1+2=3, 1+2+3=6, usw.; im Fall der ungeraden Zahlen sind es die Quadratzahlen 1, 1+3=4, 1+3+5=9 usw. (genauer gesagt ist es die 1., 2., 3. usw Partialsumme der jeweiligen Reihe).
Es gibt einen bemerkenswert einfachen Zusammenhang zwischen dem Quadrat einer Dreieckszahl einerseits und der Summe von Kuben andererseits:
(1 + 2 + … n)² = 1³ + 2³ + … n³Die folgende Figur gibt die linke Seite der Gleichung für den Fall n=5 wieder.
Und überraschend einfach lässt sich dieser Zusammenhang erklären, wenn man die hakenförmigen Flächen betrachtet, in die sich das Quadrat zerlegen lässt. Die beiden Seiten eines jeden Hakens können nämlich gegensinnig so zusammengesetzt werden, dass sich Quadrate ergeben und zwar fünf 5er-Quadrate (= 5³), vier 4er-Quadrate (= 4³) etc.:
Diese Beweisidee geht zurück auf den Mathematiker Abu Bakr al-Karaji (953 – 1029); nachzulesen in „Der mathematische Monatskalender“, Mai 2014 von Heinz Klaus Strick (Leverkusen) bei → www.spektrum.de (s.a. „Mathematics Magazine“, June 1990, p. 178).
| Nach der sogenannten Weizenkornlegende wurde dem Erfinder des Schachspiels von seinem Herrscher ein Wunsch frei gewährt. Der Erfinder wünschte sich daraufhin Weizenkörner: Auf das erste Feld eines Schachbretts wollte er ein Korn, auf das zweite Feld die doppelte Menge, also zwei, auf das dritte wiederum doppelt so viele, also vier und so weiter. | ||
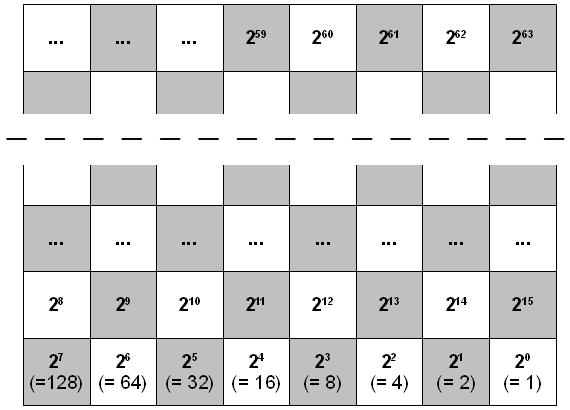 |
Es geht um die Berechnung der Summe 1+2+4+8+…x, wobei x das Ergebnis der 63. Verdopplung ist, also =263. Man sieht schnell, dass solche Mengen keinen Platz auf einem Schachbrett haben, da schon 210=1024 ist, 211=2048 usw. Trotzdem liegt die Frage nahe, wie viele Körner es insgesamt sind.
Die Folge der Zahlen 1,2,4,8,… ist jedoch keine arithmetische Reihe, und wir müssen uns nach anderen Möglichkeiten zur Berechnung der Summe umschauen.
Bilden Sie die Partialsummen 1, 1+2, 1+2+4, usw., und versuchen Sie eine Gesetzmäßigkeit zu formulieren. Notieren Sie z.B. in einer Tabelle in der oberen Zeile die Zahlen 2n und darunter jeweils die Summe bis zu dieser Zahl (=1+2+…+2n):Auch wenn man sich aufgrund der obigen Tabelle schon recht sicher ist, dass die gefundene Gesetzmäßigkeit korrekt ist, ein Beweis ist es nicht. Wir sehen nur, dass die Gesetzmäßigkeit für die Zahlen der Tabelle gilt, ob sie aber darüber hinaus Gültigkeit hat, können wir nur vermuten.
(→ Lösung)
2n: 1+…+2n:
1 2 4 8 16 32 64 128 256 512 1024 1 3 7 15
Was die Zahlenfolge 1, 2, 22, 23 usw. von einer arithmetischen Folge unterscheidet, ist, dass nicht die Differenz benachbarter Folgeglieder konstant ist sondern der Quotient: 2/1 = 22/2 = 23/22 usw. Man nennt so etwas eine geometrische Folge und die dazugehörige Summe 1+2+22+23+… eine geometrische Reihe.
Multipliziert man eine geometrische Folge oder Reihe mit dem jeweiligen Quotienten, so erhält man wieder eine geometrische Folge bzw. Reihe; Gleiches gilt für die Division. In unserem Fall der Summe 1+2+22+23+…+263 heißt das z.B.
Daraus folgt nun, dass die Differenz aus 2×(1+2+22+23+…+263) und 1+2+22+23+…+263 genau 264 − 1 ist:
A)
2 × ( 1 + 2 + 22 + 23 + … + 263 ) = 2 + 22 + 23 + 24 + … + 264 B)
( 1 + 2 + 22 + 23 + … + 263 ) / 2 = ½ + 1 + 2 + 22 + … + 262
Aber was ist andererseits für jede Zahl x die Differenz von 2x und x? Genau: 2x − x = x. Und deshalb ist
2 + 22 + 23 + 24 + … + 264 (das ist 2 × ( 1 + 2 + 22 + 23 + … + 263 ) ) − ( 1 + 2 + 22 + 23 + … + 263 ) − 1 + 264
1 + 2 + 22 + 23 + … + 263 = 264 − 1(Eine ganz andere Idee zur Herleitung dieser Summenformel zeigen wir nachher (→ hier). Und eine weitere, arithmetische Herleitung der Summenformel zeigen wir (→ hier))
Übungsaufgaben:
„Zwei Radfahrer starten in einem Abstand von 20 km und fahren aufeinander zu, jeder mit einer konstanten Geschwindigkeit von 10 km/h. Zur gleichen Zeit startet eine Fliege mit einer konstanten Geschwindigkeit von 15 km/h vom Vorderrad des einen Fahrrads und fliegt zum Vorderrad des anderen Fahrrads, dreht dann um und fliegt wieder zurück zum Vorderrad des Fahrrads, wo sie gestartet war, und fliegt auf diese Weise weiter, bis sich die beiden Fahrräder treffen. Frage: Welche Gesamtstrecke hat die Fliege zurückgelegt?“Welcher Trick ist hier gemeint, und wie hat von Neumann die Aufgabe angeblich gelöst? Führen Sie die Rechnung jeweils aus.
Als die Frage an von Neumann bei einer Party in der 1920er Jahren gestellt wurde, löste er sie, ohne erkennbar nachzudenken, und enttäuschte damit den Fragesteller: „Oh, Sie kennen den Trick schon!“ „Welchen Trick?“, fragte von Neumann, „Ich habe doch nur die geometrische Reihe summiert.“
Vollkommene Zahlen
Mit der Summenformel 1+2+…2n = 2n+1 – 1 lässt sich Euklids Formel zu Berechnung vollkommener Zahlen herleiten. (→hier an einem Zahlenbeispiel)
Vielleicht hat diese Summenformel die antiken Mathematiker überhaupt erst animiert, nach solchen Zahlen zu suchen, die jeweils Summe ihrer eigenen Teiler sind. Denn 2n+1 hat genau die (echten) Teiler 1, 2,… 2n, und die Summe dieser Teiler ist fast 2n+1. Jedenfalls sagt Euklid in Buch IX, Prop. 36:
Ist 1+2+…+2n eine Primzahl, dann ist 2n(1+2+…+2n) eine vollkommene Zahl.1+2+…+2n (= 2n+1 – 1) heißt in diesem Fall Mersenne-Primzahl. Wir wissen bis heute nicht, ob es unendlich viele Mersenne-Primzahlen bzw. vollkommene Zahlen gibt. Und wir wissen ebenfalls nicht, ob es ungerade vollkommene Zahlen gibt. Denn Euklids Formel liefert nur gerade Zahlen. Man wusste auch lange nicht, ob damit alle geraden unvollkommenen Zahlen erfasst werden – erst Euler gelang dieser Beweis.
(Beweis: Übungsaufgabe)
Das folgende Bild ist einer Szene aus „Homerun für die Liebe“ der Serie „Die Simpsons“ entnommen (Orig.: „The Simpsons: Marge and Homer Turn a Couple Play“, Staffel 17, Episode 22). Darin werden die Zuschauer im Stadion von Springfield aufgefordert eine Schätzung über die aktuelle Besucherzahl abzugeben. Auf dem Stadion-Bildschirm sind drei mögliche Antworten vorgegeben: 8128, 8208 und 8191.
 |
[…] Diese Zahlen mögen zufällig und harmlos aussehen, aber tatsächlich stellen sie eine vollkommene Zahl, eine narzisstische Zahl und eine Mersenne-Primzahl dar.
8128 gehört zu den sogenannten vollkommenen Zahlen, weil die Summe ihrer Teiler die Zahl selbst ist. Die kleinste vollkommene Zahl ist 6, weil 1, 2 und 3 nicht nur die Teiler von 6 sind, sondern sich auch zu 6 addieren. Die zweite vollkommene Zahl ist 28, denn 1, 2, 4, 7 und 14 ergeben zusammen 28. Die dritte vollkommene Zahl ist 496, die vierte ist 8128, eben die Zahl aus der Simpsons-Folge. René Descartes, der berühmte Mathematiker und Philosoph aus dem 17. Jahrhundert, sagte einmal: „Vollkommene Zahlen sind genauso selten wie vollkommene Menschen“.
8208 ist eine narzisstische Zahl. Sie enthält vier Ziffern, und wenn man von jeder dieser Ziffern die vierte Potenz bildet und die Resultate addiert, kommt wieder die Zahl selbst heraus: 84 + 24 + 04 + 84 = 8208. Die Tatsache, dass die Zahl 8208 sich so aus ihren Komponenten neu erschaffen kann, deuten die Mathematiker als eine gewisse Selbstverliebtheit, daher der Name „narzisstisch“. In der unendlichen Folge aller Zahlen gibt es weniger als hundert, die diese Eigenschaft besitzen.
8191 ist eine Primzahl, denn sie hat keine Teiler außer 1 und sich selbst, und sie heißt eine Mersenne-Primzahl, weil Marin Mersenne, ein anderer französischer Mathematiker des 17. Jahrhunderts, herausfand, dass 8191 gleich 213 – 1 ist. Allgemeiner: Mersenne-Primzahlen gehorchen dem Muster 2p – 1, wobei p eine Primzahl ist. […]
„Die Simpsons“ sind voll solcher Bezüge zur Mathematik. Simon Singh hat darüber das sehr unterhaltsame und lesenswerte Buch „Homers letzter Satz“ verfasst.
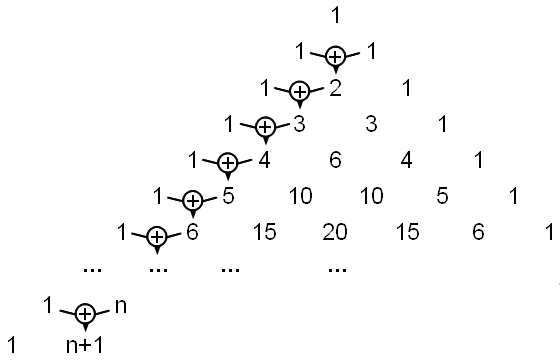
Die Dreieckszahlen kommen recht überraschend in einem ganz anderen Zusammenhang noch vor, nämlich im Pascal'schen Dreieck:
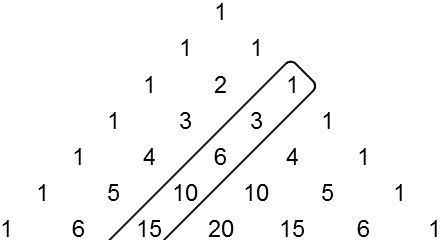 |
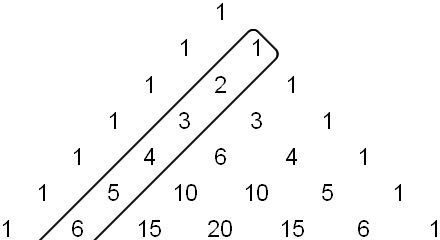 |
Zur Auffrischung: Was ist ein Pascal'sches Dreieck, und was ist daran interessant?
Wenden wir uns wieder den beiden obigen Zahlenfolgen im Pascal'schen Dreieck zu, den natürlichen Zahlen und den Dreieckszahlen. Eigentlich sehen wir ja nicht diese Zahlenfolgen selbst sondern nur ihre Anfänge. Aber wir vermuten, dass sich diese Anfänge korrekt fortsetzen würden.
Eine solche Denkweise heißt in den Naturwissenschaften Induktion. Dabei verallgemeinert man das Vorhandensein einer Eigenschaft bei bekannten Objekten auf alle Objekte dieser Art, etwa: „Alle bekannten Vögel legen Eier; also legen alle Vögel Eier“. Die verallgemeinerte Aussage bleibt aber letztlich so lange zweifelhaft, bis alle Objekte dieser Art bekannt sind und die betreffende Eigenschaft an ihnen festgestellt ist. Und dabei kann es auch vorkommen, dass die verallgemeinerte Aussage verworfen werden muss (z.B. sind nicht alle Schwäne weiß, es gibt auch schwarze).
Wie sicher sind wir also, dass z.B. nach dem obigen Anfang der natürlichen Zahlen im Pascal'schen Dreieck auch jede Fortsetzung korrekt ist? Die Berechnung weiterer Zeilen des Dreiecks liefert zumindest kein Gegenbeispiel, aber so können wir nicht alle Zahlen überprüfen!
(Überlegen Sie erst selbst, ehe Sie weiterlesen.)
Ein Blick auf die Konstruktion des obigen Dreiecks zeigt, dass sich jede der Zahlen 2, 3, 4, 5, 6 dadurch ergibt, dass die jeweils vorhergehenden Zahl zu der links von ihr stehenden 1 addiert wird – entsprechend der Konstruktionsregel des Pascal'schen Dreiecks.
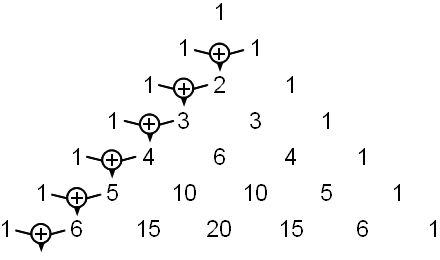 |
Mit der Variablen n formuliert heißt das: Steht in irgendeiner Zeile an zweiter Stelle die Zahl n (und 1 an erster Stelle), dann steht in der darauf folgenden Zeile an zweiter Stelle wegen der Konstruktionsregel des Pascal'schen Dreiecks: 1 + n (und an erster Stelle wieder 1).
 |
Fassen wir unsere Erkenntnisse zusammen:
Diese typische Schlussweise der Mathematik heißt vollständige Induktion; die 1. Erkenntnis nennt man den Induktionsanfang und die 2. den Induktionsschritt.
Wir brauchen wohlgemerkt beide Erkenntnisse um zu dem obigen Schluss über die gesamte Folge zu kommen. Würde die Folge nicht mit 1 beginnen sondern etwa mit 0,5, dann hätten auch alle anderen Folgeglieder die Form x,5 und wären keine natürlichen Zahlen, wie wir aufgrund der Erkenntnis (2) schlussfolgern können. Würde die Folge zwar mit 1 beginnen, aber die Nachfolger würden etwa durch Addition von 2 gebildet, dann erhielten wir nur die ungeraden natürlichen Zahlen. (Wie müssten solche Dreiecke wohl aussehen? Pascal'sche Dreiecke wären es ja nicht.)
Betrachten wir nun die Folge der Dreieckszahlen im Pascal'schen Dreieck also die Folge 1, 3, 6, 10, 15 usw., die sich direkt unterhalb der Folge der natürlichen Zahlen befindet. Wie lauten in diesem Fall Induktionsanfang und -schritt?
(Überlegen Sie erst selbst, ehe Sie weiterlesen.)
Wir bezeichnen mit Δn die n-te Dreieckszahl:
Im Pascal'schen Dreieck befindet sich eine Folge von Dreieckszahlen, die mit Δ1 beginnt (gefolgt von Δ2, Δ3, Δ4, Δ5 … so weit man rechnet).
Ist die n-te Zahl in dieser Folge die Dreieckszahl Δn, dann folgt als nächstes die Dreieckszahl Δn+1.
Begründung: Aufgrund der Konstruktionsregel des Pascal'schen Dreiecks ist die nächste Zahl nach Δn die Summe n+1+Δn.
Weiter sind wir davon ausgegangen, dass Δn=1+2+3+…+n die n-te Dreieckszahl ist, so dass für die Summe n+1+Δn gilt:
n+1+Δn = n+1 + 1+2+3+…+n = Δn+1
Beide Aussagen zusammen, der Induktionsanfang (die erste Zahl ist Δ1) und der Induktionsschritt (wenn die n-te Zahl Δn ist, dann ist die nächste Zahl Δn+1), führen in einem „Dominoeffekt“ zu der Erkenntnis, dass alle Zahlen der betreffenden Folge Dreieckszahlen sein müssen.
Diese Beweistechnik bietet sich auch für die obige Aufgabe zur Weizenkornlegende an. Dort war die Summe 1+2+22+23+…+263 zu berechnen. Betrachten wir dazu folgende Veranschaulichung als Punktmuster:
|
(⇒ Präsentation als pdf-Datei) |
Wir sehen hier anschaulich, dass die betrachtete Summe stets 1 weniger ist als diejenige 2er-Potenz, die als nächstes zu addieren wäre. Und man hat insbesondere den Eindruck, dass sich dieses geometrische Muster beliebig fortsetzen lässt: 20+21+…+2n = 2n+1-1.
Was wir diesen Mustern mit Sicherheit entnehmen können, ist der Induktionsanfang:
Die Summenformel 20+…+2n = 2n+1-1 liefert ein richtiges Ergebnis, wenn für n die Zahl 1 eingesetzt wird: 1+2=4-1. (Und sie ist auch richtig für n=2, n=3, … soweit man rechnet).
Der Induktionsschritt lautet:
Wenn die Summenformel 20+…+2n = 2n+1-1 für eine natürliche Zahl n richtig ist, dann stimmt sie auch für die nächste Zahl n+1.Um das einzusehen, betrachten wir die fragliche Summe von 20 bis 2n+1. In ihr ist die Summe von 20 bis 2n enthalten, von der wir annehmen, dass die Summenformel ein richtiges Ergebnis liefert: 20+…+2n = 2n+1-1. Damit gilt:
20 + … + 2n+1
= 20+…+2n + 2n+1
= 2n+1-1 + 2n+1
= 2·2n+1-1
= 2n+2-1
Verbinden wir zwei Punkte auf einer Kreislinie durch eine Strecke, dann teilt diese die Kreisfläche in zwei Gebiete. Verbinden wir drei Punkte, dann erhalten wir vier Gebiete, und bei vier Punkten acht Gebiete. Wie viele Gebiete erhalten wir wohl (maximal) bei fünf Punkten.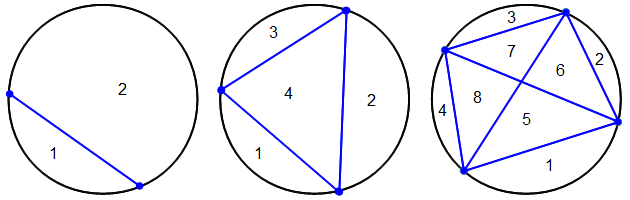
Punkte auf der Kreislinie: 2 3 4 5 6 … Anzahl der Gebiete: 2 4 8
(Überlegen Sie erst selbst, ehe Sie weiterlesen.)
Erwartungsgemäß finden wir bei → fünf Punkten doppelt so viele Gebiete wie bei vier Punkten, also 16.
Aber wir wissen noch nicht, weshalb sich die Anzahl der Gebiete von Punkt zu Punkt verdoppelt. Deshalb ist diese Erwartung bislang nur eine Spekulation.
Wir könnten jetzt Überlegungen anstellen, wie es zur Verdopplung der Gebietszahlen kommt. Aber das können wir uns sparen, denn schon das nächste Beispiel mit → sechs Punkten auf der Kreislinie zeigt, dass unsere Spekulation falsch war: Wir erhalten in diesem Fall höchstens 31 Gebiete.
13, 17, 23, 31 sind allesamt Primzahlen. Die Liste ist insofern unvollständig, als es noch weitere Primzahlen zwischen den berechneten gibt (19 und 29), aber dieser Anfang lässt immerhin hoffen, dass die Formel auch weiterhin ausschließlich Primzahlen liefert, was man für n = 5, 6 und 7 schnell mit positivem Ergebnis nachrechnen kann.
n: 1 2 3 4 5 … n2 + n + 11: 13 17 23 31
Übungsaufgabe: Beweisen Sie die Gleichung
(1 + 2 + … + n)² = 1³ + 2³ + … + n³(→ s.o.) durch vollständige Induktion.
Diese Beweistechnik erinnert an den sogenannten Dominoeffekt: Wenn der erste Stein so umfällt, dass er den zweiten umstößt, dann fallen der Reihe nach alle Steine um. Es war Blaise Pascal, der als Erster diese Beweismethode beschrieb (17. Jh.). Ende des 19. Jh. wurde sie unter der Bezeichnung vollständige Induktion zur grundlegenden Beschreibung der natürlichen Zahlen herangezogen. Unabhängig voneinander leisteten dies Richard Dedekind und Giuseppe Peano. Eine übliche Formulierung dieser Dedekind-Peano-Axiome lautet:
Das Standardmodell dieser Axiome ist die geordnete Menge 0→1→2→3…. Doch auch andere Mengen erfüllen die obigen Axiome, z.B. die geraden Zahlen (mit 0): 0→2→4→6…. Der Nachfolger von 0 ist hier jedoch 2 und nicht 1.
Darüber hinaus ist auch die Verwendung des Zeichens 0 nicht zwingend. Wir beginnen beim Zählen im Alltag ohnehin mit 1. Entscheidend ist nur, dass es ein Anfangselement gibt. Allgemein nennen wir deshalb jede Menge N mit einem Element α und einer Abbildung σ: N → N ein Modell der Dedekind-Peano-Axiome, wenn die folgenden Axiome erfüllt:
In der Mathematik nennt man eine solche Abbildung, die bijektiv ist und die jeweiligen Strukturen berücksichtigt einen Isomorphismus; die Zielmenge ist dann isomorph zur Definitionsmenge (salopp gesagt: dasselbe in grün). Formal: Ist M irgendein Modell der Dedekind-Peano-Axiome mit der (eigenen) Nachfolgerabbildung τ, dann gibt es einen Isomorphismus i:
0 → 1 → 2 → 3 → 4 … 0 → 1/2 → 2/3 → 3/4 → 4/5 …
| i(σ(n)) = τ(i(n)). |
Es ist ungewohnt, ein Nicht-Standardmodell wie die geraden Zahlen als gleichwertiges Modell zu ![]() anzusehen. Aber wir haben immerhin gesehen, dass die Modelle im Wesentlichen gleich sind. Entscheidend ist nun, dass Mengen mit wesentlich anderen Strukturen keine Modelle der Dedekind-Peano-Axiome sind. Betrachten wir etwa die zyklische Struktur
anzusehen. Aber wir haben immerhin gesehen, dass die Modelle im Wesentlichen gleich sind. Entscheidend ist nun, dass Mengen mit wesentlich anderen Strukturen keine Modelle der Dedekind-Peano-Axiome sind. Betrachten wir etwa die zyklische Struktur
Auch sie ist insofern unendlich, als man unbegrenzt Nachfolger bilden kann, wobei man sich jedoch sozusagen im Kreise dreht. Diese Struktur ist kein Modell der Dedekind-Peano-Axiome, weil 0 ∈ σ(
0 → 1 ↑ ↓ 3 ← 2
0 → 1/2 → 2/3 → 3/4 … 1 → 2 → 3 …Es ist 0∈
Eine nicht-leere Menge nennt man wohlgeordnet, wenn jede nicht-leere Teilmenge (und damit auch die Menge selbst) ein kleinstes Element hat. Voraussetzung ist selbstverständlich, dass alle Elemente der Menge durch eine Ordnungsrelation vergleichbar sind.
Beispiele sind: die natürlichen Zahlen ℕ oder etwa die Menge {0; 1; 2} oder die Menge {√2; 2; π; 4,1} – jeweils mit der üblichen ≤-Relation.
Gegenbeispiele sind: die ganzen Zahlen ℤ, die rationalen Zahlen ℚ und die reellen Zahlen ℝ – ebenfalls mit der üblichen ≤-Relation .
Die Formulierung lässt noch offen, ob es mehrere kleinste Elemente gibt. Aber da es uns hier um Zahlen und die übliche ≤-Relation geht, sieht man schnell, dass es eben nicht mehrere geben kann. Wären nämlich a und b zwei kleinste Zahlen einer Menge M (a,b ∈ M), dann wäre für alle m ∈ M sowohl a ≤ m also auch b ≤ m. Ersteres beinhaltet a ≤ b (da b ∈ M) und Letzteres b ≤ a (da a ∈ M). Somit wäre a = b (Antisymmetrie). Wir setzen im Weiteren daher voraus, dass die Ordnung antisymmetrisch ist.
Also hat jede wohlgeordnete Menge ein eindeutig bestimmtes kleinstes Element. Wir nennen es Anfangselement, α.
Des Weiteren können wir in wohlgeordneten Mengen den Nachfolger eines Elements m definieren, sofern es größere Elemente als m gibt. Ist nämlich die Menge der größeren Elemente nicht leer, Tm = { t ∈ M | m < t } ≠ ∅, dann hat sie ein eindeutig bestimmtes kleinstes Element. Das nennen wir den Nachfolger von m. Der Nachfolger ist sozusagen das kleinste aller größeren Elemente.
Daraus folgt:
Gibt es in einer wohlgeordneten Menge kein größtes Element, dann hat jedes Element einen eindeutig bestimmten Nachfolger.
Es liegt hier nahe, die natürlichen Zahlen einfach als wohlgeordneten Menge ohne größtes Element beschreiben zu wollen. Das wäre viel einfacher als die Dedekind-Peano-Axiome, aber es ist leider nicht richtig. Dennoch lohnt sich der Ansatz, wie wir gleich sehen werden.
Bereits oben am Schluss des Abschnitts über die Dedekind-Peano-Axiome haben wir gezeigt, dass die Menge {0, 1/2, 2/3, 3/4, ..., 1, 2, 3, ...} diesen Axiomen nicht genügt; das Induktionsaxiom ist nämlich verletzt. Aber diese Menge ist wohlgeordnet, und sie hat kein größtes Element. Daher genügen diese beiden Forderungen nicht zur Charakterisierung der natürlichen Zahlen. Aber es gibt eine einfache Zusatzforderung, durch die solche Mengen ausgeschlossen werden: Es darf nur ein Element geben, das nicht Nachfolger eines anderen ist: das Anfangselement. Damit lassen sich die natürlichen Zahlen nun charakterisieren:
Ist M eine wohlgeordnete Menge ohne größtes Element und mit nur einem Element, das nicht Nachfolger eines anderen ist, dann genügt M mit der durch die Wohlordnung induzierten Nachfolger-Funktion den Dedekind-Peano-Axiomen.
Beweis:
Wir haben bereits gezeigt, dass eine wohlgeordnete Menge ein Anfangselement α hat und dass jedes Element einen eindeutigen Nachfolger hat, wenn es kein größtes Element gibt. Also bleibt noch zu zeigen, dass die Nachfolger-Funktion injektiv ist und dass α kein Nachfolger eines anderen Elements ist. Vor allem aber ist zu zeigen, dass das Induktionsaxiom erfüllt ist. Und dafür benötigen wir die Forderung, dass α das einzige Element ist, das nicht Nachfolger eines anderen ist.
Übungsaufgabe: Zeigen Sie: Ist M eine wohlgeordnete Menge ohne größtes Element und mit nur einem Element, das nicht Nachfolger eines anderen ist, dann ist
Kommen wir schließlich zum Induktionsaxiom. Wir setzen wieder voraus, dass M eine wohlgeordnete Menge ist ohne größtes Element und mit nur einem Element, das nicht Nachfolger eines anderen ist. Außerdem sei S eine Teilmenge von M, in der α enthalten ist und mit jedem s ∈ S auch der Nachfolger s' ∈ S. Wir zeigen, dass unter diesen Voraussetzungen S = M gilt. Dafür verwenden wir das Beweisverfahren durch Widerspruch:
Angenommen, es sei S ≠ M. Dann ist M\S = {m ∈ M | m ∉ S} ≠ ∅. Aufgrund der Wohlordnung hat M\S ein kleinstes Element; wir nennen es σ. Dieses kann nicht α sein, da nach Voraussetzung α ∈ S und damit α ∉ M\S. Daher ist σ der Nachfolger eines Elements ρ ∈ M, und es gilt damit ρ < σ. Nun ist σ das kleinste Element in M\S und folglich ρ ∉ M\S also ρ ∈ S. Aber für die Elemente in S gilt, dass auch ihre Nachfolger darin enthalten sind, so dass σ als Nachfolger von ρ auch in S enthalten sein müsste, σ ∈ S. Das steht im Widerspruch zu σ ∈ M\S. Also gilt doch S = M.
Also erfüllt eine wohlgeordnete Menge ohne größtes Element und mit nur einem Element, das nicht Nachfolger eines anderen ist, alle Dedekind-Peano-Axiome, und der Beweis der obigen Aussage ist somit abgeschlossen.
Umgekehrt lässt sich zeigen (was wir hier nicht tun), dass jedes Modell der Dedekind-Peano-Axiome eine wohlgeordnete Menge mit den beiden genannten Eigenschaften ist. Damit sind die beiden Beschreibungen der natürlichen Zahlen äquivalent. Der Vorteil der Dedekind-Peano-Axiome liegt für Mathematiker darin, dass das Induktionsaxiom bereits enthalten ist. Denn Beweise durch Induktion gehören zu den Grundfertigkeiten eines Mathematikers. Die Beschreibung der natürlichen Zahlen als wohlgeordnete Menge hat hingegen den didaktischen Vorteil, dass sie intuitiver ist, weil sie gerade das Induktionsaxiom nicht benötigt.
Historische Anmerkung: Laut Hans Rohrbach hat Erhard Schmidt in seinen Vorlesungen zur „Einführung in die höhere Mathematik” ab 1920 die natürlichen Zahlen als eine wohlgeordnete Menge wie oben charakterisiert. Siehe: H. Rohrbach: „Das Axiomensystem von Erhard Schmidt für die Menge der natürlichen Zahlen”; in: Mathematische Nachrichten, 4. Band, 1950/51, S. 315-321.
Auf Galilei geht folgende Überlegung zu Quadratzahlen (1, 4, 9, …) zurück:
Wir wissen, dass jede Quadratzahl eine natürliche Zahl ist. Umgekehrt sind aber die meisten natürlichen Zahlen keine Quadratzahlen (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …). Die Menge der Quadratzahlen ist also (in moderner Sprechweise ausgedrückt) eine echte Teilmenge der natürlichen Zahlen, weshalb man geneigt ist zu sagen, es gäbe weniger Quadratzahlen als natürliche Zahlen.
Andererseits können wird die Quadratzahlen der Größe nach ordnen und nummerieren:
Damit haben wir jeder natürlichen Zahl eindeutig eine Quadratzahl zugeordnet und umgekehrt jeder Quadratzahl eindeutig eine natürliche Zahl. Die jeweiligen Mengen sind also bijektiv aufeinander abbildbar, weshalb man geneigt ist zu sagen, es gäbe genauso viele Quadratzahlen wie natürliche Zahlen.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. … ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ … 1 4 9 16 25 36 49 64 81 100 121 …
| ⇒ Ein Widerspruch! |
|---|
Unabhängig von der Frage nach mehr, weniger oder ebenso vielen Elementen, kann man nämlich untersuchen, welche Mengen sich so durchnummerieren lassen wie die Quadratzahlen. Z.B. gilt das für die geraden sowie die ungeraden Zahlen aber auch für die ganzen Zahlen:
|
|
 |
Übungsaufgabe:
„Hilberts Hotel“ ist ein Gedankenexperiment von David Hilbert, um die Unendlichkeit der natürlichen Zahlen zu veranschaulichen.
[Youtube:] Hilbert's Infinite Hotel – 60-Second Adventures in Thought (4/6)
Man könnte nun annehmen, dass Abzählbarkeit eine Eigenschaft unendlicher Mengen sei. Aber Cantor konnte auch zeigen, dass die reellen Zahlen nicht abzählbar sind, dass es verschiedene Arten von Unendlichkeit gibt. Sein Argument ist das 2. Cantor'sche Diagonalverfahren:
|
(⇒ Präsentation als pdf-Datei) |
Cantor zeigte, dass keine Auflistung reeller Zahlen vollständig sein kann, weil man mithilfe einer solchen Liste eine Zahl konstruieren könnte, die darin nicht enthalten wäre. Ist beispielsweise eine Liste von Dezimalzahlen zwischen 0 und 1 gegeben, dann bildet man aus der Diagonalen eine Zahl und verändert jede ihrer Ziffern hinterm Komma. Diese neue Zahl unterscheidet sich von der ersten Zahl in der Liste an der ersten Nachkommastelle, von der zweiten Zahl an der zweiten Nachkommastelle usw. Sie kommt also in der Liste nicht vor.
Übungsaufgabe: Konstruieren Sie zu folgendem Anfang einer Liste die ersten Stellen einer Zahl, die darin nicht vorkommt:
Nachdem die reellen Zahlen offenbar anders unendlich sind als die natürlichen, stellt sich zum einen die Frage,
„A ist so unendlich wie B“ soll demnach heißen, dass A und B unendlich sind und es eine Bijektion zwischen ihnen gibt.
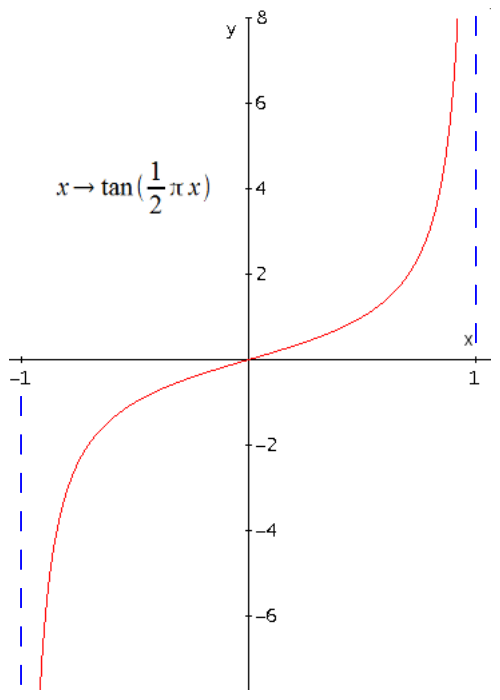 Im Fall der natürlichen Zahlen können wir dabei immer noch an ein Nummerieren denken. Und im Fall der reellen Zahlen können wir jetzt z.B. sagen, dass die Menge der Zahlen im Intervall (−1; +1) so unendlich ist wie die Menge der reellen Zahlen insgesamt, da die Funktion x → tan(½ π x) eine bijektive Abbildung von (−1; +1) in die reellen Zahlen ist. (Eine weitere Menge, die so unendlich ist wie die reellen Zahlen, ist die Menge aller Teilmengen der natürlichen Zahlen, d.i. die Potenzmenge der nat. Zahlen).
Im Fall der natürlichen Zahlen können wir dabei immer noch an ein Nummerieren denken. Und im Fall der reellen Zahlen können wir jetzt z.B. sagen, dass die Menge der Zahlen im Intervall (−1; +1) so unendlich ist wie die Menge der reellen Zahlen insgesamt, da die Funktion x → tan(½ π x) eine bijektive Abbildung von (−1; +1) in die reellen Zahlen ist. (Eine weitere Menge, die so unendlich ist wie die reellen Zahlen, ist die Menge aller Teilmengen der natürlichen Zahlen, d.i. die Potenzmenge der nat. Zahlen).Für diese Relation gelten folgende Eigenschaften („Mathepedia: Gleichmächtigkeit“):
- A ~ B („A und B sind gleichmächtig“)
- gilt genau dann, wenn es eine Bijektion zwischen den Mengen A und B gibt.

0 = {∅} 1 = {{0}, {–}, {♦}, {•} …} 2 = {{0, 1}, {–(1) , –(2)}, {♦(1) , ♦(2)}, {•(1) , •(2)} …} ⋮ ℵ₀ = {{0, 1, 2, 3, …}, {0, 2, 4, 6, …}, {0², 1², 2², 3², …}, …} ⋮
Übungsaufgabe: Betrachten Sie die Ersatz-Zahlwortreihe
a, b, c, d, e, f, aa, ab, ac, ad, ae, af, ba, …, bf, …, fa, …, ff, aaa, aab, …
Unter einem Anfangsabschnitt Ax verstehen wir die Menge der Ersatz-Zahlwöter von a bis x.
(a) Wie heißen die Abschnitte, die gleichmächtig sind zu den Mengen A7={1, 2, 3, 4, 5, 6, 7}, A1={1}, A43={1, 2, 3, …, 43} ? (→ Antwort)
(b) Wie heißt die Kardinalzahl von M={a, e, h, l, o, t, x} unter Verwendung der üblichen Zahlen und wie in der Ersatz-Zahlwortreihe? (→ Antwort)
(c) Geben Sie eine Menge an, die bei Verwendung der Ersatz-Zahlwortreihe die Kardinalzahl: i) b, ii) f, iii) aa hat. (→ Antwort)
Damit war prinzipiell die Möglichkeit gegeben, die natürlichen Zahlen durch etwas Allgemeineres zu begründen, sie dadurch zu definieren. Welche große Bedeutung diesem Fortschritt um 1900 beigemessen wurde, zeigen folgende Zitate von David Hilbert (→ Hilbertprogramm) und Bertrand Russel:
„Aus dem Paradies, das Cantor uns geschaffen, soll uns niemand vertreiben können.“
[David Hilbert: Über das Unendliche, Mathematische Annalen 95 (1926), S. 170]
„Wir denken natürlich, daß die Menge der Paare etwas von der Zahl 2 Verschiedenes ist. Aber über die Menge der Paare besteht keine Unsicherheit. An ihr kann nicht gezweifelt werden, und ihre Definition macht keine Schwierigkeiten, während auf der anderen Seite die Zahl 2 in irgend einem Sinne etwas Metaphysisches ist, von dem wir niemals das sichere Gefühl haben, daß es existiert oder daß wir es ergründet haben. Es ist daher klüger, uns mit der Menge der Paare zu begnügen, deren wir sicher sind, als einer problematischen Zahl 2 nachzujagen, die sich uns immer listig entziehen wird. Demgemäß stellen wir folgende Definition auf: Die Zahl einer Menge ist die Menge aller ihr äquivalenten Mengen. Die Zahl eines Paares ist somit die Menge aller Paare.“
[Bertrand Russell: Einführung in die mathematische Philosophie, Kap.2)]
Allerdings wurde die Mengenlehre nicht von allen Mathematikern so euphorisch begrüßt. Einer ihrer prominentesten Kritiker im 19. Jh. war Leopold Kronecker. Bekannt ist sein Ausspruch:
„Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.“Er war damit ein Vorläufer des mathematischen Kronstruktivismus, einer mathematik-philosophische Richtung, die sich in Abgrenzung zur formalistischen Richtung nach Hilbert im 20. Jh. entwickelte. Er hätte sich durch die folgenden Probleme sicher bestätigt gesehen:
[H. Weber: Leopold Kronecker. In: Jahresbericht der Deutschen Mathematiker-Vereinigung 2 (1893), S.19]
 Mengenvorstellungen, die nur anschaulich begründet sind, führen schnell zu widersprüchliche Aussagen, wie bei Galilei. Nehmen wir z.B. die Klasse der Einermengen, 1, und bilden daraus die Menge {1}. Dann ist diese Menge ebenfalls eine Einermenge und müsste deshalb der Klasse 1 angehören: {1}∈1. Umgekehrt gilt sozusagen für x-beliebige Objekte x∈{x}, also auch 1∈{1}. Fasst man 1∈{1} und {1}∈1 zusammen, dann folgt: …1∈{1}∈1∈{1}…
Mengenvorstellungen, die nur anschaulich begründet sind, führen schnell zu widersprüchliche Aussagen, wie bei Galilei. Nehmen wir z.B. die Klasse der Einermengen, 1, und bilden daraus die Menge {1}. Dann ist diese Menge ebenfalls eine Einermenge und müsste deshalb der Klasse 1 angehören: {1}∈1. Umgekehrt gilt sozusagen für x-beliebige Objekte x∈{x}, also auch 1∈{1}. Fasst man 1∈{1} und {1}∈1 zusammen, dann folgt: …1∈{1}∈1∈{1}…
| ⇒ Ein Widerspruch! |
|---|
Man kann einen Barbier definieren als einen, der alle die rasiert, und nur diese, die sich nicht selbst rasieren.Die auf den ersten Blick sinnvoll erscheinende Barbier-Definition führt genauso zu einem Widerspruch wie die Russell-Menge.
Die Frage ist: Rasiert der Barbier sich selbst?
Im Zuge der „Neuen Mathematik“ wurde der Mathematikunterricht an Grundschulen mit Mengenlehre und Kardinalzahlen eröffnet, während der traditionelle Rechenunterricht, den man damit ersetzte, mit Zählen und Rechnen angefangen hatte. Die Größen des Sachrechnens wie Gewichte, Längen, Flächen, Volumina, Zeit definierte man in Analogie zu den Kardinalzahlen als Äquivalenzklassen. Den Längen etwa wurde die Kongruenzrelation für geometrische Strecken zugrundegelegt, und die Länge einer Strecke als die Klasse der zu ihr kongruenten (deckungsgleichen) Strecken festgelegt. Für die anderen Größen verwendete man jeweils andere Vergleichsrelationen (z.B. „gleich schwer“ für Gewichte).
Anders als die geometrische Kongruenzrelation ist der Vergleich realer Objekte aber keine Äquivalenzrelation. Wir müssen dabei nämlich stets die Grenze der Messgenauigkeit berücksichtigen. Ist der Unterschied zweier Objekte (Gewichtsdifferenz, Längendifferenz, …) zu klein, können wir ihn nicht mehr feststellen. (Ansonsten wäre die Kopie der Kopie der Kopie etwa des Ur-Meters oder des Ur-Kilogramms in Paris genauso lang bzw. schwer wie dieses und wir bräuchten kein Eichamt.) Wegen der Ungenauigkeit des Messens kommt es aber vor, dass z.B. a und b gleichlang erscheinen ebenso wie b und c, jedoch zwischen a und c ein Unterschied feststellbar ist: a~b und b~c aber nicht a~c. (Angemessener wäre die Interpretation einer Größe als Abbildung, die realen Objekten jeweils ein Intervall der reellen Zahlen zuordnet).